66. Метод множителей Лагранжа

Рассмотрим частный случай общей задачи нелинейного программирования (1), (2), предполагая, что система ограничений (2) содержит только уравнения, отсутствуют условия неотрицательности переменных и и — функции, непрерывные вместе со своими частными производными

(16)

(17)

В курсе математического анализа задачу (16), (17) называют задачей на условный экстремум или классической задачей оптимизации.

Чтобы найти решение этой задачи, вводят набор переменных называемых Множителями Лагранжа, составляют функцию Лагранжа

(18)

Находят частные производные и и рассматривают систему уравнений

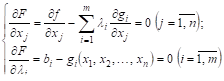(19)

С неизвестными Всякое решены системы уравнений (19) определяет точку в которой может иметь место экстремум функции . Следовательно, решив систему уравнений (19), получают все точки, в которых функция (16) может иметь экстремальные значения. Дальнейшее исследование найденных точек проводят таК Же, как и в случае безусловного экстремума.

Таким образом, определение экстремальных точек задачи (16), (17) методом множителей Лагранжа включает следующие этапы:

1. Составляют функцию Лагранжа.

2. Находят частные производные от функции Лагранжа по переменным и и приравнивают их нулю.

3. Решая систему уравнений (19), находят точки, в Которых Целевая функция задачи может иметь экстремум.

3. Среди точек, подозрительных на экстремум, находят такие в которых достигается экстремум, и вычисляют значения функции (16) в этих точках.

1.28. По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве изделий I способом затраты равны руб., а при изготовлении изделий II способом они составляют руб. Определить, сколько изделий каждым из способов следует изготовить так чтобы общие затраты на производство продукции были минимальными.

Решение. Математическая постановка задачи состоит в определении минимального значения функции

(20)

При условиях

(21)

(22)

Сначала найдем решение задачи, используя ее геометрическую интерпретацию. Областью допустимых решений исходной задачи является отрезок прямой АВ (рис. 18), а линиями уровня — окружности с центром в точке Е(-2; -4).

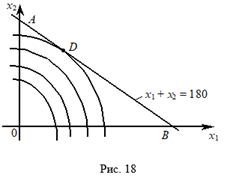
Проводя из точки Е окружности разных радиусов, видим, что минимальное значение целевая функция принимает в точке D. Чтобы найти координаты этой точки, воспользуемся тем, что угловой коэффициент к окружности в точке D совпадает с угловым коэффициентом прямой и, следовательно, равен -1. Рассматривая как неявную функцию от и дифференцируя уравнение окружности, имеем

или

Приравнивая полученное выражение числу -1, получаем одно из уравнений для определения координат точки D. Присоединяя к нему уравнение прямой, на которой лежит точка D, Имеем систему

Откуда Это означает, что если предприятие изготовит 91 изделие I технологическим способом и 89 изделий II способом, то общие затраты будут минимальными и составят 17278 руб.

Решим теперь задачу, используя метод множителей Лагранжа. Найдем минимальное значение функции (20) при условии (21), т. е. без учета требования неотрицательности переменных. Для этого составим функцию Лагранжа

Вычислим ее частные производные по и приравняем их нулю:

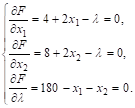
Перенося в правые части первых двух уравнений И приравнивая их левые части, получим

или

Решая последнее уравнение совместно с уравнением находим и , т. е. получили координаты точки D, удовлетворяющей условиям (22). Эта точка является подозрительной на экстремум. Используя вторые частные производные, можно показать, что в точке D функция F имеет условный минимум. Этот результат и был получен выше.

Следует отметить, что такой же результат мы получим и в том случае, если исследование на условный экстремум функции F сведем к исследованию на безусловный экстремум функции F1, полученной из F в результате ее преобразований. А именно: если из уравнения связи (21) найдем и подставим это выражение в (20), то получим функцию одной переменной :

Найдем стационарную точку этой функции из уравнения или откуда Так же как и выше, устанавливаем, что в данной точке функция F имеет минимальное значение.

1.29. Найти точки экстремума функции при уcловии

Решение. Составим функцию Лагранжа

Найдем ее частные производные по и приравниваем их к нулю.

В результате получим систему уравнений

(23)

Из первого и второго уравнений имеем . Решая это уравнение совместно с третьим из системы (23), находим . Таким образом, в точке (5/2; 5/2) данная функция может иметь условный экстремум. Чтобы определить, достигается ли в этой точке условный экстремум, нужно провести дополнительные исследования. В частности, используя вторые частные производные, можно показать, что в этой точке функция имеет условный минимум и

Метод множителей Лагранжа можно применять и в том случае, когда условия связи представляют собой неравенства. Так, если требуется найти экстремум функции при условии то сначала следует найти точки безусловного экстремума функции из уравнений , затем среди этих точек отобрать те, координаты которых удовлетворяют условию связи G (X) <Ь, и, наконец, определить точки, удовлетворяющие системе уравнений

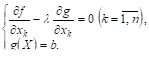
Точки, найденные в результате решения этой системы, вместе с точками, определенными на первом этапе и удовлетворяющими условию , подлежат дальнейшему исследованию, как и при нахождении безусловного экстремума.

< Предыдущая		Следующая >