58. Общая и основная задачи линейного программирования

В предыдущем параграфе были рассмотрены примеры задач линейного программирования. Во всех этих задачах требовалось найти максимум или минимум линейной функции при условии, что ее переменные принимали неотрицательные значения и удовлетворяли некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные неравенства, так и линейные уравнения. Каждая из этих задач является частным случаем общей задачи линейного программирования.

Определение 1.1. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

(8)

При условиях

(9)

(10)

(11)

Где - заданные постоянные величины и .

Определение 1.2. Функция (8) называется Целевой функцией (или Линейной формой) задачи (8) - (11), а условия (9) - (11) — Ограничениями данной задачи.

Определение 1.3. Стандартной (или Симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где K = M и L=N.

Определение 1.4. Канонической (или Основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где K=0 и L=п.

Определение 1.5. Совокупность чисел , удовлетворяющих ограничениям задачи (9) - (11), называется Допустимым решением (или Планом).

Определение 1.6. План , при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется Оптимальным.

Значение целевой функции (8) при плане Х будем обозначать через . Следовательно, X* — Оптимальный план задачи, если для любого Х выполняется неравенство [соответственно ].

Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.

Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно в общем случае уметь, во-первых, сводить задачу минимизации функции к задаче максимизации, во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот, в-третьих, заменять переменные, которые не подчинены условию неотрицательности.

В том случае, когда требуется найти минимум функции , можно перейти к нахождению максимума функции , поскольку .

Ограничение-неравенство исходной задачи линейного программирования, имеющее вид «£», можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида «³» — в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство

Преобразуется в ограничение-равенство

(12)

А ограничение-неравенство

— в ограничение-равенство

(13)

В то же время каждое уравнение системы ограничений

Можно записать в виде неравенств:

(14)

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.

Отметим, наконец, что если переменная , не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными и , приняв .

1.4. Записать в форме основной задачи линейного программирования следующую задачу: найти максимум функции при условиях

Решение. В данной задаче требуется найти максимум функции, а система ограничений содержит четыре неравенства. Следовательно, чтобы записать ее в форме основной задачи, нужно перейти от ограничений-неравенств к ограничениям-равенствам. Так как число неравенств, входящих в систему ограничений задачи, равно четырем, то этот переход может быть осуществлен введением четырех дополнительных неотрицательных переменных. При этом к левым частям каждого из неравенств вида «£» соответствующая дополнительная переменная прибавляется, а из левых частей каждого из неравенств вида «³» вычитается. В результате ограничения принимают вид уравнений:

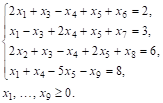
Следовательно, данная задача может быть записана в форме основной задачи таким образом: максимизировать функцию при условиях

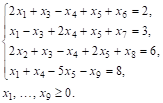
1.5. Записать задачу, состоящую в минимизации функции при условиях

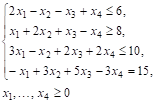
В форме основной задачи линейного программирования.

Решение. В данной задаче требуется найти минимум целевой функции, а система ограничений содержит три неравенства. Следовательно, чтобы записать ее в форме основной задачи, вместо нахождения минимума функции F нужно найти максимум функции F1 = - F при ограничениях, получающихся из ограничений исходной задачи добавлением к левым частям каждого из ограничений-неравенств вида «£» дополнительной неотрицательной переменной и вычитанием дополнительных переменных из левых частей каждого из ограничений-неравенств вида «³».

Следовательно, исходная задача может быть записана в форме основной задачи линейного программирования так: найти максимум функции при условиях

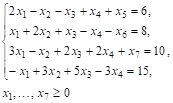
1.6. Записать в форме стандартной задачи линейного программирования следующую задачу: найти максимум функции при условиях

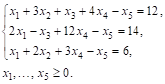
Решение. Методом последовательного исключения неизвестных сведем данную задачу к следующей: найти максимум функции при условиях

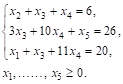
Последняя задача записана в форме основной для задачи, состоящей в нахождении максимального значения функции при условиях

Целевая функция задачи преобразована с помощью подстановки вместо и их значений в соответствии с уравнениями системы ограничений задачи.

< Предыдущая		Следующая >