57. Примеры задач линейного программирования

1.1. Для изготовления трех видов изделий А, В И С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице 1. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида.

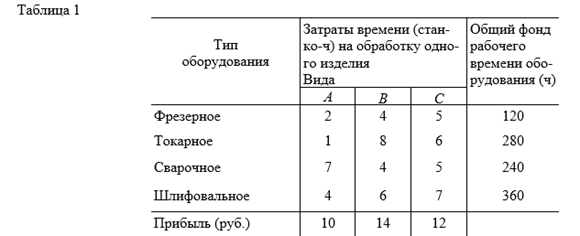
Требуется определить, сколько изделий, и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Составить математическую модель задачи.

Решение. Предположим, что будет изготовлено единиц изделий вида А, единиц — вида В и единиц — вида С. Тогда для производства такого количества изделий потребуется затратить станко-часов фрезерного оборудования.

Так как общий фонд рабочего времени станков данного типа не может превышать 120, то должно выполняться неравенство

Аналогичные рассуждения относительно возможного использования токарного, сварочного и шлифовального оборудования приведут к следующим неравенствам:

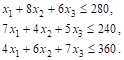
При этом так как количество изготовляемых изделий не может быть отрицательным, то

(1)

Далее, если будет изготовлено единиц изделий вида А, единиц изделий вида В и единиц изделий вида С, то прибыль от их реализации составит

Таким образом, приходим к следующей математической задаче: дана система

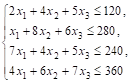(2)

Четырех линейных неравенств с тремя неизвестными И линейная функция относительно этих же переменных

(3)

Требуется среди всех неотрицательных решений системы неравенств (2) найти такое, при котором функция (3) принимает максимальное значение. Как это сделать, будет показано в дальнейшем.

Линейная функция (3), максимум которой требуется определить, вместе с системой неравенств (2) и условием неотрицательности переменных (1) образуют математическую модель исходной задачи.

Так как функция (3) линейная, а система (2) содержит только линейные неравенства, то задача (1) - (3) является задачей линейного программирования.

1.2. Продукцией городского молочного завода является молоко, кефир и сметана, расфасованное в бутылки. На производство 1 т молока, кефира и сметаны требуется соответственно 1010, 1010 и 9450 кг молока. При этом затраты рабочего времени при разливе 1 т молока и кефира составляют 0,18 и 0,19 машино-ч. На расфасовке 1 т. сметаны заняты специальные автоматы в течение 3,25 ч. Всего для производства цельномолочной продукции завод может использовать 136000 кг молока. Основное оборудование может быть занято в течение 21,4 машино-ч, а автоматы по расфасовке сметаны — в течение 16,25 ч. Прибыль от реализации 1 т молока, кефира и сметаны соответственно равна 30, 22 и 136 руб. Завод должен ежедневно производить не менее 100 т молока, расфасованного в бутылки. На производство другой продукции не имеется никаких ограничений.

Требуется определить, какую продукцию и в каком количестве следует ежедневно изготовлять заводу, чтобы прибыль от ее реализации была максимальной. Составить математическую модель задачи.

Решение. Предположим, что молочный завод будет ежедневно производить тонн молока, тонн кефира и тонн сметаны. Тогда ему для изготовления этой продукции необходимо кг молока.

Так как завод может использовать ежедневно не более 136000 кг молока, то должно выполняться неравенство

Аналогичные рассуждения, проведенные относительно возможного использования линий разлива цельномолочной продукции и автоматов по расфасовке сметаны, позволяют записать следующие неравенства:

Так как ежедневно должно вырабатываться не менее 100 т молока, то . Далее, по своему экономическому смыслу переменные и могут принимать только лишь неотрицательные значения: Общая прибыль от реализации тонн молока, тонн кефира и тонн сметаны равна Руб. Таким образом, приходим к следующей математической задаче: дана система

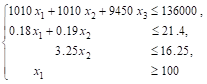(4)

Четырех линейных неравенств с тремя неизвестными , , и линейная функция относительно этих же переменных

(5)

Требуется среди всех неотрицательных решений системы неравенств (4) найти такое, при котором функция (5) принимает максимальное значение. Так как система (4) представляет собой совокупность линейных неравенств и функция (5) линейная, то исходная задача является задачей линейного программирования.

1.3. На швейной фабрике ткань может быть раскроена несколькими способами для изготовления нужных деталей швейных изделий. Пусть при J-м варианте раскроя 100 м2 ткани изготовляется деталей I-го вида , а величина отходов при данном варианте раскроя равна м2. Зная, что деталей I-го вида следует изготовлять штук, требуется раскроить ткань так, чтобы было получено необходимое количество деталей каждого вида при минимальных общих отходах. Составить математическую модель задачи.

Решение. Предположим, что по J-му варианту раскраивается сотен м2 ткани. Поскольку при раскрое 100 м2 ткани по J-му варианту получается деталей I-Го вида, по всем вариантам раскроя из используемых тканей будет получено

Деталей I-го вида. Так как должно быть изготовлено деталей данного вида, то

Общая величина отходов по всем вариантам раскроя ткани составит

Таким образом, приходим к следующей математической задаче: найти минимум функции

(6)

При условии, что ее переменные удовлетворяют системе уравнений

(7)

И условию неотрицательности

Сформулированная задача является задачей линейного программирования, так как функция (6) линейная, а система (7) содержит только лишь линейные уравнения.

< Предыдущая		Следующая >