03. Математика в гуманитарных науках

Около 100 лет назад американский экономист Ирвинг Фишер установил, что во всем мире едва насчитывалось пятьдесят достойных внимания книг и статей по математической экономике. Сегодня не только в экономике, но и во всех остальных общественных науках положение в корне изменилось; каждый год появляются тысячи новых книг в огромном потоке математической литературы. Причиной тому — все возрастающее понимание преимуществ выражения на языке математики концепций, которые прежде излагались только словесно.

Степень использования математики в различных областях знания различна. Все, что охватывается демографией и экономикой, выражается явно количественными показателями, а это неизбежно требует широкого применения математики. Кроме того, в общественных науках становится все более очевидным, что одно лишь словесное описание сложных систем и их взаимосвязей приводит к обобщениям, которые с трудом поддаются анализу, сравнению и применению. В еще большей мере это относится к словесной формулировке теорий о функционировании таких систем. Подобные трудности в основном преодолеваются при замене слов математическими выражениями. С одной стороны, ряд проблем, которые, казалось бы, абсолютно не связаны друг с другом, как, например, проблема исследования различных систем образования и планирование капиталовложений, тождественны в математическом смысле. С другой стороны, даже в вопросах, где представления весьма неопределены, и где трудно получить какие-либо точные данные, с помощью математики удается вскрыть важные закономерности.

Рискуя быть уличенным в излишнем упрощенчестве, можно все же сказать, что общественные науки, несмотря на все их разнообразие, имеют лишь две основные области исследования. Первая из них — это точное описание функционирования различных общественных систем и взаимосвязей их отдельных частей, например брак в родовой общине или вклад, вносимый сталелитейной промышленностью в показатель валовой продукции технически развитой страны. В исследованиях такого рода анализируется структура системы. Вторая область исследований относится к проблемам управления, т. Е. к рассмотрению влияния сознательно применяемых методов на функционирование различных социальных структур, и к анализу рациональных процессов, которые лежат в основе определения направления развития. В этих исследованиях анализируются и изучаются принимаемые решения.

На рис. 1 отображена схема взаимодействия четырех основных потоков математической модели британской экономики. В основной части модели — схема реальных потоков (). Спрос на предметы потребления и темп роста этого спроса в сочетании с экспортом и темпом его роста (В Средней части схемы, справа) определяют капиталовложения, необходимые для требуемого роста выпуска продукции. Уровень выпуска продукции определяется конечным спросом для потребления, капиталовложений и экспорта, а также текущими потребностями в сырье и топливе. Для заданных уровней выпуска продукции и ресурсов рабочей силы распределение труда и капитала в промышленности определяется соображениями эффективного использования ресурсов. Система внешней торговли () имеет аналогичное начало из двух частей и, кроме очевидного воздействия цен внешнего рынка и торговых балансов на импорт, влияет на уровень выпуска отечественной продукции и на цены внутреннего рынка. В системе цен () показано непосредственное их влияние на размеры потребительского спроса. Обратная связь возникает из-за влияния уровня заработной платы, производительности труда и стоимости, добавленной в процессе производства (в Средней части схемы, слева), так что цены внутреннего рынка и общие затраты потребителей в конце цикла вычислений вновь пересчитываются. Наконец, поскольку квалификация рабочей силы не менее важна, чем основные фонды, четвертая система (…..) демонстрирует взаимосвязанные факторы образования и профессиональной подготовки, которые взаимодействуют как с общей численностью рабочей силы (в терминах производительности труда и спроса на квалифицированную рабочую силу), так и со спросом на предметы потребления (в терминах затрат на образование).

В обеих вышеуказанных областях исследований к сходным проблемам применяются одни и те же математические методы. Если необходим эмпирический анализ дискретных наблюдений, большую пользу извлекают из конечной математики, прежде всего из матриц, матричной алгебры и уравнений в конечных разностях. Там, где, наоборот, требуется

Чисто теоретический анализ, и данные представляют скорее информацию непрерывного характера, а не дискретные «биты», использование дифференциального и интегрального исчисления и уравнений в частных производных имеет много преимуществ. В нижеследующих примерах показано применение обоих математических методов.

В число демографических исследований входит анализ структуры и вероятного роста народонаселения. Для прогнозирования будущей структуры народонаселения, предположив, что картина рождаемости и выживания не изменяется, требуется знать, во-первых, число людей различных возрастов, проживающих на определенную дату, во-вторых, показатель выживания для определенного интервала времени, начиная с этой даты; в-третьих, число людей, родившихся за тот же самый период времени от разных возрастных групп. Третья совокупность показателей дает, между прочим, пример того вида неточности, которая может вкрасться в количественные данные, используемые в общественных науках. В действительности мужья и жены часто принадлежат к различным возрастным группам, и деторождение зависит как от этого фактора, так и от индивидуальной способности женщин к деторождению. Однако в математической модели, которая будет здесь рассмотрена, детей классифицируют лишь по возрастным группам матерей.

При таком способе анализа удобнее всего представлять изменения, происходящие за определенный период, в виде прямоугольной таблицы, или матрицы (табл. 2). Вначале данные о возрастном составе населения располагают в трех столбцах. Затем строят собственно квадратную матрицу, где каждой возрастной группе соответствуют одна строка и один столбец. В клетках верхней строки матрицы приводится число детей, родившихся за выбранный период у матерей соответствующих возрастных групп. Затем число индивидуумов каждой возрастной группы, выживающих до конца этого периода, а, следовательно, переходящих из своей возрастной группы в следующую, вносится по диагонали, идущей вниз слева направо и расположенной непосредственно под главной диагональю в том же направлении.

Теперь можно приступить к обработке данных. Если разделить число новорожденных и число выживающих индивидУУмов, записанных в каждом столбце матрицы, на число индивидуумов той же возрастной группы в 1940 г. (см. матрицу б), то получим (соответственно) нормы рождаемости и выживания. Эти коэффициенты запишем затем в матрице В. Если теперь столбец с числом индивидуумов по возрастным группам в 1940 г. умножить справа на матрицу коэффициентов В, то результат, который получится для каждой возрастной группы, даст предполагаемый состав популяции к концу выбранного периода. Предположим, что этот период составляет Х лет; если требуется получить структуру народонаселения по истечении 2Х лет, то столбец исходной численности по возрастным группам умножается на квадрат матрицы коэффициентов. Когда необходимо выяснить структуру по истечении 3Х лет, матрицу-множитель нужно возвести в третью степень и т. Д. Здесь операции, выполняемые над нашими данными, просто названы умножением. Математики знают, что этот процесс по существу есть умножение матрицы коэффициентов на столбец цифр именно справа, поскольку при умножении матриц неприменим коммутативный закон обычного арифметического умножения.

При прогнозах такого рода предполагается, что картина рождаемости и выживания остается неизменной в течение всего рассматриваемого периода времени. Эта предпосылка является вторым примером расхождений, существующих между моделью и действительностью. Тем не менее, даже такая далекая от реальности модель проливает свет на данную проблему. Операции с этой жесткой моделью показывают, что если показатели рождаемости и смертности в самом деле окажутся неизменными, то со временем будут достигнуты как стабильная возрастная структура, так и постоянный темп роста народонаселения.

Разумеется, такая неизменная матрица коэффициентов весьма мало правдоподобна, так как рождаемость и смертность зависят либо от случайных, либо от систематически действующих факторов или же от тех и других одновременно. Поэтому исследователь стремится приблизиться к реальности, варьируя величины, входящие в матрицу коэффициентов: этот процесс известен как усложнение модели. Не представляет труда сформулировать условия, при которых численность населения будет стремиться к какому-то верхнему или нижнему пределу, следовательно, методы, применяемые демографами, могут быть распространены на изучение проблем, касающихся экологии и эпидемиологии.

Следует особо отметить, что процесс математизации помогает выявить определенное сходство в СТруктуре многих проблем, хотя они и представляются различными. МатриЦА, прогнозирующая развитие народонаселения, была использована для демОгРафических целей. Точно так же можно прогнозировать развитие популяций, состоящих из неодушевленных предметов, таких, как, скажем, телеграфные столбы, железнодорожные вагоны или жилые дома, и тогда эта модель может быть использована при изучении проблем материальных запасов в промышленности или городского строительства. В таких случаях нормы рождаемости заменяются нормами вложений, а показатель смертности — показателем износа. Какой бы ни была возрастная структура первоначального запаса, модель показывает необходимое пополнение или замену, обеспечивающую надлежащий запас в течение любого желаемого отрезка времени.

Для этнографов представляет интерес также исследование родственных связей со всей сложностью установления картины браков и поколений, кланов, фратрий, племен и, наконец, классовой структуры и социальных сдвигов. В исследованиях такого рода часто бывает удобно пользоваться для обработки данных уравнениями в конечных разностях. Классический пример социального напластования существовал у Нэтчез — племени американских индейцев бассейна Миссисипи. Племя Нэтчез разделялось на два основных класса: аристократов и неимущих. Аристократы в свою очередь делились на три сословия: на людей «солнца» (высшее сословие), «благородных» (среднее сословие) и «почтенных», которые еще считались аристократами, но были всего на одну ступеньку выше неимущих — «парий».

Исходя из описаний путешественников-очевидцев, брачные законы, существовавшие у племени Нэтчез, вносили своего рода постоянный социальный фермент. В каждом браке один из партнеров (муж или жена) всегда выбирался из класса «парий». При этом ребенок, родившийся от матери аристократки, принадлежал к сословию своей матери. Так, ребенок матери из сословия «солнца», «благородных» или «почтенных» и отца из «парий» также становился «солнцем», «благородным» или «почтенным». Ребенок же матери из «парий» и отца из «солнца» должен был принадлежать к сословию, на ступень ниже отцовского, и в данном случае он становился лишь «благородным». Подобное перемещение в низшее сословие осуществлялось последовательно, так что отпрыск матери из «парий» и отца из «благородных» становился «почтенным», а матери из «парий» и отца из «почтенных» — просто «парием». На низшей ступени этой социальной лестницы у мужчины и женщины из сословия «парий» ребенок относился к «париям».

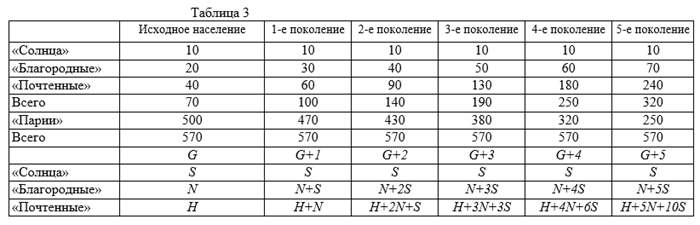
Племя Нэтчез давно исчезло с лица земли, но исследователи классовых структур продолжают интересоваться, могла ли такая сложная социальная система обладать естественной устойчивостью. Для математизации этой задачи необходимо предположить, что общая численность племени Нэтчез стабильна, что каждый индивидуум из этого племени вступает в брак ровно один раз и от каждого такого брака рождается один мальчик и одна девочка. Если с учетом всех этих факторов построить математическую модель, то становится очевидным, что такая классовая структура может быть устойчивой лишь в том предположении, что с самого начала отсутствуют сословия «солнца» и «благородных». В противном случае, уже через несколько поколений появилось бы такое многочисленное потомство аристократов, что для браков не нашлось бы больше неимущих (см. табл. 3).

Приведенная математическая модель дает основание предположить, что племя Нэтчез в действительности не имело стабильной классовой структуры. Однако из-за недостаточности фактических данных нельзя быть уверенным в правильности этого вывода. Если изменить модель с учетом того, что возможно различное количество браков, приходящееся на одного индивидуума, или различная деторождаемость, скажем в результате брака представителя сословия «солнца» с «парием» и брака «пария» с «парием», или с учетом таких совершенно не включенных в модель элементов, как быстрый рост численности племени Нэтчез в результате завоеваний и ассимиляции, то все эти изменения могли бы привести к совсем другому результату.

В совершенно иной области исследований экономисты, желающие провести анализ темпов роста, сталкиваются с проблемой приведения в определенную систему бесчисленного количества операций, связанных с производством, потреблением, накоплением и внешней торговлей. Один из способов построения такой стройной системы — это рассмотрение экономики в виде сложной системы взаимосвязанных «счетов»; теоретически этого можно добиться с помощью огромной матрицы, в которой каждой паре «строка — столбец» соответствовал бы один такой «счет». Доход можно было бы записать по строкам, а расходы — по столбцам. В действительности если все потоки какой-либо экономической системы подробно занести в единую матрицу, то она оказалась бы неимоверно большой и ее практически невозможно было бы использовать в расчетах. Единственное решение — это объединение «счетов» в укрупненные группы. В замкнутой экономике можно, например, свести сложную картину деятельности к трем взаимосвязанным счетам: «счет производства», «счет потребления» и «счет накопления» (рис. 2).

Рис. 2

В экономике, описанной моделью такого типа, счет производства получает деньги со счета потребления за продаваемые потребительские товары и оказываемые услуги, а со счета накопления — за продаваемые средства труда. Затем со счета производства на счет потребления передается та часть выручки за реализуемую продукцию, которая соответствует доходу. Этот доход для счета потребления является единственным видом поступлений, которые делятся затем на две неравные части. Большая часть тратится на приобретение дополнительных количеств потребительских товаров и услуг (что снова приводит к возникновению потока со счета пОТребления на счет производства), а меньшая переходит в сбережения (с соответствующим потоком на счет накопления). Для того чтобы система была замкнутой, эти сбережения выплачиваются затем со счета накопления на счет производства за дополнительные средства труда.

Две гипотезы в этой модели очевидны. Согласно первой, общий доход в точности равен сумме затрат на предметы потребления и сбережений, согласно второй, сбережения в свою очередь в точности равны затратам на средства труда. Две другие гипотезы, хотя и не столь очевидные, при анализе оказываются ключевыми в этой замкнутой модели экономики. Одна из них состоит в том, что население сберегает определенную долю своих доходов (обозначим ее через A), вторая — что существует определенный коэффициент пропорциональности между затратами на средства труда, т. Е. дополнительными капиталовложениями, и ростом «выхода» со счета производства, т. е. дополнительной продукцией. (Этот коэффициент обозначен B)

Любая замкнутая экономика, основывающаяся на таких предпосылках, может расти лишь с постоянным темпом, который характеризуется отношением . Для того чтобы увЕЛичить темп роста, система должна либо сберегать и затем инвестировать большую часть своего дохода (т. е. увеличить A), либо, наоборот, требовать меньше капиталовложений на единицу выпускаемой продукции (т. е. уменьшить B), либо осуществить и то и другое одновременно. В качестве примера возьмем следующие численные величины параметров: A (норма сбережений) равно 10% от дохода, а B (указанный выше коэффициент пропорциональности) равно 2,5%. Тогда отношение даст темп роста 4%. Но если A увеличить до 12,5%, а B снизить до 2, то темп роста народного хозяйства возрастет с 4 до 5%.

Можно привести еще один пример использования математики в анализе социальных явлений — это пример из сферы образования. Беспокойство за наличие в обществе достаточного количества преподавателей в будущем требует анализа соотношения между числом учителей и учеников. В простейшем случае можно считать само собой разумеющимся, что число выпускников при любой системе образования пропорционально числу учителей, занятых в этой системе. Увеличение числа учителей в свою очередь зависит от доли (она предполагается постоянной) учащихся данной системы, которые становятся учителями, и доли (также предполагается постоянной) учителей, выбывших по причине смерти, ухода на пенсию или перемены рода занятий.

Число выпускников, приходящихся в этом примере на одного учителя, можно обозначить через A, долю учащихся, которые становятся учителями, — через B, а долю выбытия учителей — через G. Тогда легко вывести формулу для расчета относительного прироста учителей (обозначим его D). Эта формула имеет следующий вид: . На первый взгляд может показаться, что здесь математизировано лишь совершенно очевидное. Уравнение говорит только о том, что если потребуется больше учителей, то необходимо либо 1) предложить существующим учителям выпускать большее количество учащихся (т. е. увеличить A), либо 2) убедить большее число выпускников избрать профессию учителя (т. е. увеличить B); либо 3) уменьшить Убытие Учителей (т. е. снизить G), либо, наконец, выполнять все эти мероприятия одновременно.

СведЕНие задачи к математическим отношениям позволяет не только вскрыть самоочевидные факты. Если все вышеуказанные требования отобразить с помощью графика (рис 3), то можно проанализировать дополнительно еще ряд моментов, влияющих друг на друга. Предположим, что положение в обществе таково, что практически никак нельзя повлиять на постоянное снижение числа учителей (скажем, ни одно учебное заведение не примет снова на работу тех учителей, которые

Сменили профессию). При таких обстоятельствах исключаются какие бы то ни было существенные изменения коэффициента, G однако на величину A и B еще можно воздействовать. Каковы будут тогда результаты от повышения заработной платы учителям? Это, безусловно, привело бы к тому, что большее число выпускников избрало профессию учителя (увеличение B), а также к упрочению статуса учителя, значит, к повышению эффективности его труда (рост A).

В самом деле, если предположить, что между A и B и заработной платой учителя существует гиперболическая зависимость, то при очень низкой оплате труда учителя не станут, работать, а выпускники не захотят стать учителями и, наоборот, при очень высокой оплате и учителя будут работать эффективнее и количество выпускников, которые решат стать учителями, будет приближаться к своему максимуму. В таком случае соотношение между A и B является линейным, и если его изобразить на нашем графике, то возникает возможность вычислить для всех значений A и B соответствующие им ставки заработной платы.

Все предыдущие примеры были связаны с описанием человеческого общества без рассмотрения тех механизмов, которые определяют его современное состояние. Исследование различных общественных явлений с учетом этих механизмов требует анализа методов принятия решений.

Процесс принятия решений может быть в значительной степени сформулирован и изучен на языке математики. Кроме классического аппарата математики, для принятия решений используются новые методы, как-то: линейное программирование, теория игр и теория статистических решений. Однако необходимо предварительно разграничить решения, принимаемые в условиях определенности, от решений, принимаемых в условиях неопределенности. В рамках этих двух категорий необходимо различать решения, относящиеся к одному периоду времени, от тех решений, которые связаны с линией поведения в течение нескольких периодов.

Примером первой категории и первой подкатегории (т. е. решение одноэтапное, принимаемое в условиях определенности) служит задача о диете, где выбирается соответствующий режим питания при минимальных затратах. В этой задаче необходимая диета определяется в виде некоторого минимального числа показателей питательной ценности, таких, как количество белков, жиров, углеводов, витаминов, калорийность и т. П. Продукты питания, цены которых, известны, характеризуются разными значениями показателей питательной ценности. Сколько тогда нужно купить каждого пищевого продукта, чтобы получить требуемый рацион питания при минимальных затратах?

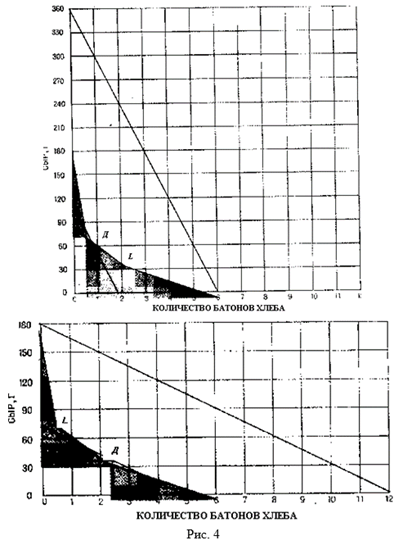
(Рис. 4) Рацион, требующий минимальных затрат, показывает, что даже решение, принятое в условиях определенности не всегда приемлемо. В этом примере допускается, что хлеб и сыр характеризуются разными сочетаниями трех требуемых показателей питательной ценности (например, 60 Г сыра содержат столько же белка, сколько шесть батонов хлеба). Нанеся эти три пропорции на график, получим ломаную линию (L), каждая точка которой удовлетворяет всем требованиям, касающимся питательной ценности. Теперь необходимо найти самое дешевое сочетание двух продуктов питания. Если 360 г сыра стоят столько же, сколько шесть батонов хлеба (верхний график), то самый дешевый рацион (точка Д) разумен: на каждые полбатона хлеба приходится несколько более 60 г сыра. ЕсЛИ же заменить это соотношение цен на обратное (нижний график), то самый дешевый рацион должен содержать неприемлемое количество дешевого хлеба по сравнению с количеством дорогого сыра.

Если взять упрощенный случай (рассмотреть только два продукта питания и только три показателя питательной ценности), то задачу можно интерпретировать геометрически на плоскости. По каждой из двух осей координат откладывается один из двух выбранных продуктов питания (рис. 4). При N продуктах питания такое же геометрическое построение может быть сделано в N-мерном пространстве: с ростом П возрастает и число вычислений, необходимых для отыскания решения.

На практике решение задачи о диете минимальной стоимости сводится к выбору всего лишь нескольких продуктов питания, т. е. к весьма неудовлетворительной диете. Обычно эта задача ставится очень узко, например не принимается в расчет вес продуктов, входящих в самый дешевый рацион, а часто оказывается, что этот вес очень велик. Недавно диетологи установили, что ограничение веса ежедневно потребляемой пищи приводит к значительно более раЗНообразной диете без существенного изменения ее стоимости. Эта проблема слишком узкой постановки задач раскрывает характерную для всех сложных расчетов особенность: математические методы являются «буквальными». С их помощью решаются задачи в том виде, как они поставлены, и уже дело исследователя проследить за их формулировкой.

Если решение принимается в условиях неопределенности, необходимо использовать теорию вероятностей и математическую статистику.

СОчетание различных теоретических методов с фактическими материалами в области общественных наук приводит к получению полезных моделей реальных ситуаций. Если модель используется в свою очередь для решения нескольких задач, то в результате формируется определенная политика. Именно по этой причине, я думаю, в настоящее время во многих странах строятся крупные количественные модели национальных экономических систем, предназначенные для практического использования. Народное хозяйство можно рассматривать как систему, преобразующую информацию в решение. Современная количественная модель экономики, при условии, что она достаточно подробна и реальна, может предоставить много полезной информации лицам, принимающим решения по дальнейшему развитию экономики.

В Кембриджском университете была создана численная модель народного хозяйства Англии. На первом этапе была сконструирована модель для случая устойчивого экономического роста, начиная с 1970 г. Эта модель основывалась на конкретных предположениях об уровне жизни в Англии к 1970 г., а также о темпах дальнейшего развития народного хозяйства. Экономические следствия из этих предпосылок представлены в виде балансов. Во-первых, даются балансы производства и потребления по 31 группе продуктов, выделенных в модели. Во-вторых, приводятся балансы доходов и расходов в соответствующих отраслях производства. Три других баланса завершают наш ряд: это баланс спроса и предложения на рабочую силу, баланс накоплений и капиталовложений и баланс внешнеэкономических расчетов (внешняя торговля Англии).

Переменные величины модели записаны в квадратной матрице, состоящей из 253 пар строк-столбцов (каждый из них есть счет, на котором отражаются поступления в какую-либо отрасль или сектор экономики страны или распределение ее продукции), а также соответствующих цен и натуральных показателей. Всю совокупность данных создатели модели назвали «матрицей общественных счетов». Используя эту матрицу, получаются результаты, по крайней мере, совместимые с арифметической и бухгалтерской точкой зрения.

Следует отметить, что одним из главных преимуществ экономических моделей является то, что с их помощью можно выявить результаты любых сделанных нами предположений. Мы можем, например, построить «замкнутую» систему и наблюдать за ее «естественным» развитием. При заданных начальных значениях с помощью модели можно проследить за тем, как в будущем произойдет изменение целого ряда переменных. Однако, при переходе от фактического состояния на сегодняшний день к прогнозируемому состоянию мы чаще всего сосредоточиваем свой интерес на средствах достижения такого положения вещей, которое вряд ли наступит «естественно». Существует много вопросов подобного рода: о сокращении безработицы, увеличении числа людей с высшим и средним образованием, вопрос о том, как избежать повторных кризисов в платежных балансах. Для каждого из них мы должны сделать модель в некотором отношении «открытую», добавив к ней новую особенность — точную формулировку поставленной цели. Тогда модель покажет, как осуществляется сбалансированная система при предположении, что поставленные цели достигнуты. Между тем по мере увеличения размеров нашей исходной модели приходится решать, практичнее ли добавлять новые категории или лучше вводить подмодели. Более многообещающим представляется введение подмоделей. Например, можно представить себе децентрализованную систему, в которой подмодель для топливной промышленности и энергетики или подмодель финансовой деятельности строилась бы и использовалась специалистами по топливу или финансам, обладающими всеми необходимыми знаниями. Другое преимущество метода подмоделей состоит в том, что в них могут быть отражены положения, когда в отдельных отраслях производства происходят изменения, в то время как построение единой модели требует жестких соотношений между затратами и выпуском, полностью исключающих подобные изменения.

Хотя матрица общественных счетов вначале предназначалась только для отображения экономических аспектов общественной жизни Англии, впоследствии выявилась тенденция ее неуклонного расширения. При установлении той роли, которую играют труд, капитал и изобретения в производстве товаров потребления и в сфере обслуживания, например, оказалось необходимым рассмотреть влияние не только различных профессий, но также и отношения общества к исследованиям и нововведениям. Вопрос о влиянии различных профессий привел к изучению систем общего и специального образования, а последние два вопроса привели в область социальной психологии.

В реальной жизни развитие таких систем может оказаться неравномерным — либо из-за присущей им тенденции к колебаниям, либо потому, что они лишь в ограниченной мере могут оправиться от ряда естественных возмущений, которые неизбежно воздействуют на них. Но подобно своим биологическим и техническим аналогам социально-экономические системы обладают устройствами автоматического регулирования (примером таких устройств в экономике может служить механизм ценообразования). Однако нередко эти механизмы не очень исправно выполняют свои функции, частично потому, что их цели ограничены, частично вследствие того, что они функционируют на основе ограниченной информации. Именно поэтому во всех странах в большей или меньшей сТЕпени пытаются разработать меры, улучшающие механизмы регулирования.

Выше уже отмечалось, что сочетание модели с совокупностью целей порождает политику; когда же политика сочетается с системами регулирования, то возникает план действий. Этот план в свою очередь комбинируется с происходящими событиями, давая всем нам наш опыт социально-экономической жизни. Этот опыт снова используется (в виде «обратной связи») для изменения теорий, которых мы придерживаемся, фактов, рассматриваемых нами как относящиеся к делу, целей, кажущихся нам правильными, и регулирующих систем, которые мы считаем эффективными. При изменении этих факторов опыт используется для модификации наших моделей, политики и планов действия. И так продолжается беспрестанно. Можно надеяться, что в один прекрасный день благодаря аппарату математики принимаемые решения станут основываться несколько больше на знаниях и несколько меньше на догадках и что мир, в котором мы живем, будет функционировать немного лучше и меньше будет зависеть от непредвиденных событий.

< Предыдущая		Следующая >