24. Интегрирование по частям и замена переменной в определенном интеграле
Ввиду того, что интеграл ![]() Есть ПерВообразная от
Есть ПерВообразная от ![]() , можно написать:
, можно написать:
![]()
С другой стороны, в силу формулы Ньютона — Лейбница имеем:
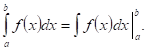
Этими двумя соотношениями выявляется точный характер связи между определенным и неопределенным интегралами.
Формула Ньютона — Лейбница показывает, что для вычисления определенного интеграла мы получили теперь хороший способ — неопределенное интегрирование. Нам уже известно, что правила интегрирования суммы и произведения постоянной на функцию имеют место и в определенном интеграле. Теперь мы рассмотрим правила интегрирования по частям и замены переменной.
Оказывается, что и эти правила неопределенного интегрирования могут быть непосредственно применены к определенному интегралу.
I. Правило интегрирования по частям:
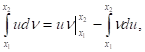 (A)
(A)
Где U и V — Функции НЕзависимой переменной.
Доказательство. Имеем:
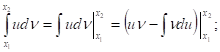
Отсюда непосредственно и следует доказываемая формула.
Вместо того чтобы до конца довести неопределенное ИнтегрироВание по частям, а затем выполнить двойную подстановку, можно сразу воспользоваться формулой (А).
Предварительное полное отыскание неопределенного интеграла требует более громоздких выкладок.
II. Правило замены переменной (подстановки).
Если в интервале ![]() функции
функции ![]() ,
, ![]() и
и ![]() непрерывны и
непрерывны и ![]()
![]() то
то
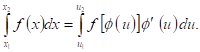 (Б)
(Б)
Доказательство. Преобразуем неопределенный интеграл ![]() при помощи подстановки
при помощи подстановки ![]()
![]()
Где ![]() — первообразная от функции
— первообразная от функции ![]()
Рассматривая U как функцию от Х, определяемую зависимостью ![]() , получим:
, получим:
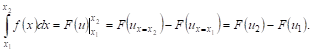
С другой стороны,
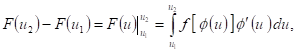
И мы приходим к равенству (Б).
ИЗ формулы (Б) видно, что подынтегральное выражение Преобразуется так же, как и в случае неопределенного интеграла. Что же КАсается пределов интегрирования, то заданные пределы X1 и Х2 связаны с новыми И1 и U2 так же, как заданная переменная Х с Новой переменной И.
Итак, вместо того чтобы, выполнив при помощи замены переменНОй неопределенное интегрирование, вернуться к первоначальной Переменной, а затем вычислить двойную подстановку в данных преДЕлах, можно сразу взять двойную подстановку в новых Пределах. Результат — значение определенного интеграла — получится ТОт же, а выкладок потребуется меньше.
Новые пределы интегрирования И1 и U2 являются корнями уравнений ![]() и
и ![]() относительно неизвестной И.
относительно неизвестной И.
Часто замена переменной в определенном интеграле производится по формуле ![]() , а по формуле
, а по формуле ![]() , выражающей НовУю переменную через заданную. Тогда новые пределы И1 и и2 сразу определяются по формулам
, выражающей НовУю переменную через заданную. Тогда новые пределы И1 и и2 сразу определяются по формулам
![]()
При этом теорема о замене переменной заведомо будет Справедлива, если функция ![]() в интервале
в интервале ![]() монотонна и Имеет ПроизВодную, отличную от нуля; тогда и обратная функция
монотонна и Имеет ПроизВодную, отличную от нуля; тогда и обратная функция ![]() будет обладать теми же свойствами.
будет обладать теми же свойствами.
Пример. Выведем формулу для интеграла, взятого по симметричному интервалу ![]()
![]()
В случаях, когда подынтегральная функция четна и нечетна. Представим этот интеграл так:
![]()
ЗамЕНив переменную интегрирования в первом интеграле в правой части по формуле ![]() , получим:
, получим:
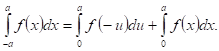
Таким образом,
![]()
Подынтегральная функция в правой части равна нулю, если ![]() — функция нечетная, и равна
— функция нечетная, и равна ![]() , еСли
, еСли ![]() — функция четная. Следовательно,
— функция четная. Следовательно,
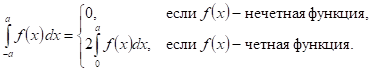
Эти формулы очень полезны. Можно, например, сразу сказать, не производя вычислений, что
![]()
Рекомендуем читателю выяснить геометрический смысл выведенных формул.
| < Предыдущая | Следующая > |
|---|