21. Простейшие свойства определенного интеграла, его геометрический смысл и оценка

Далее везде предполагается, если не сказано противное, что рассматриваемые функции — непрерывные.

Теорема I (об интеграле суммы). Интеграл от суммы конечногО числа функций РавеН сумме интегралов от слагаемых функций:

Где U, V, ..., W — функции независимой переменной Х.

Доказательство. Обозначим интеграл в левой части равенства через I. По определению интеграла имеем:

Где — Соответственно значения функций U, V, ..., W В какой-нибудь точке интервала , а . Воспользовавшись теоремой о пределе суммы, будем иметь:

Или

Что и требовалось доказать.

Теорема II (о вынесении постоянного множителя). ПостояННый множитель подынтегральной функции можно вынести за символ интеграла:

Где U — Функция аргумента Х, с — Константа.

Доказательство. Обозначим интеграл в левой части равенства через I. По определению интеграла имеем:

Вынося постоянную С сначала за знак суммы, а потом за символ предела, получим:

Что и требовалось доказать.

Изменение направления и разбиение интервала интегрирования. ГеомЕТрический смысл интеграла. До сих пор мы предполагали, что нижний предел интеграла меньше верхнего, или, как говорят, что интервал интегрирования направлен вправо. Ничто не мешает нам, однако, в общем определении интеГрала считать, что A>b, т. Е. что интервал интегрирования направлен влево. При этом при разбиении интервала интегрирования на части точками мы будем иметь (рис. 5):

И следовательно, все разности будут отрицательными. Если мы теперь рассмотрим два интеграла

и

И составим для НИх интегральные суммы при одном и том же разбиении интервала на частичные и при одном и том же выборе промежуточных точек, то ясно, что эти суммы будут отличаться друг от друга только знаком. Таким образом, мы получаем теорему:

Теорема III (о перестановке пределов). Если верхний и нижний пределы интеграла поменять местами, то интеграл изменит знак:

Вследствие теоремы III мы в дальнейшем при изучении интеграла

Будем считать, что А<B, ибо если А>B, то с помощью изменения знака подынтегральной функции данный интеграл сводится к интегралу, у которого нижний предел меньше верхнего.

Совершенно ясно также, что если верхний и нижний пределы ИнТегрирования совпадают, т. е. если , то такой интеграл нужно считать равным нулю:

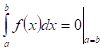или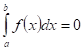

С геометрической точки зрения это означает, что если конец основания трапеции совместить с его началом, то трапеция Превращаетcя в прямолинейный отрезок — ординату .

Теорема IV (о разбиении интервала интегрирования). Если интервал иНТегрирования разбит НА две части и , то

(*)

ДоказаТЕльство. Так как предел интегральной суммы не зависит, от споСОба разбиения интервала НА части, будем дробить его так, чтобы точка С всегда была точкой деления. При этом интегральную сумму можно ПредстаВить так:

Где в первой сумме в правой части собраны все элементы, соответствующие точкам деления интервала [А, С], а во второй сумме — элементы, соответствующие точкам деления интервала . И первая и вторая суммы суть интегральные суммы для функции , соответствующие интервалам и . Если число точек деления неограниченно возрастает, а длина наибольшего частичного интервала СТремится к нулю для всего интервала , то же самое, очеВиДно, будет выполняться и для интервалов и ; при этом первая сумма стремится к интегралу в пределах от А до С, а вторая — к интегралу в пределах от С до B, и мы получаем требуемое равенство.

Равенство (*) справедливо и в том случае, когда точка С лежит вне интервала , справа от него или слева от него (при условии, конечно, что функция непрерывна в иЛи в , соответственно).

Пусть . По доказанному, так как B лежит между А и С,

Откуда

Меняя местами пределы второго интеграла в правой части, получим:

Что и требовалось доказать.

Аналогично доказывается, что равенство (*) имеет место и при .

Из доказанной теоремы непосредственно следует, что если — Как угодно расположенные числа в интервале непрерывности функции , то

(**)

Теорема IV выражает так называемое свойство аддитивности определенного интеграла.

Теорема V (о знаке интегРАла). Если подынтегральная функция в интервале интегрироВАния сохраняет постоянный знак, то интеграл представляет собой число того же знака, что и функция.

Доказательство. Пусть в интервале . Тогда в интегральной сумме

Все слагаемые положительны, и значит, , а предел положительной величины не может быть отрицателен, т. Е.

В данном случае он не может быть и нулем; действительно, обозначая через Т наименьшее значение функции в замкнутом интервале, получим:

Ясно, что , и следовательно, . Поэтому величина , остающаяся при всех П большей, чем положительное число , не может иметь предела, равного нулю.

В силу теоремы IV заключение теоремы V сохраняется и для функции, имеющей в интервале конечное число нулей.

Если подынтегральная функция в интервале интегрирования меняет знак, то интеграл от нее может быть и положительным числом, и отрицательным, и равным нулю.

Свойство определенного интеграла, вытекающее из теоремы V, следует иметь в виду при решении задач. Например, находя с помощью интеграла площадь криволинейной трапеции, необходимо учитывать ее расположение относительно основания. В случае, когда трапеция целиком лежит над осью Ох, интеграл от ординаты выражает площадь; в случае, когда трапеция целиком лежит под осью Ох, интеграл, будучи отрицательным, выражает площадь трапеции, взятую с отрицательным знаком. Наконец, в случае, когда трапеция лежит и над осью Ох и под ней, для отыскания ее площади нужно отдельно вычислить интегралы, выражающие площади ее частей, расположенных над осью абсцисс, отдельно — интегралы, выражающие площади частей, расположенных под осью абсцисс, и затем взять сумму их абсолютных величин.

Геометрический смысл интеграла. Условимся площади криволинейной трапеции, расположенной над осью Ох, приписывать знак плюс, а расположенной под осью Ох — Знак минус. Тогда, очевидно, в силу теоремы IV и V определенный интеграл от функции будет суммой алгебраических площадей (т. е. снабженных определенными знаками) криволинейных трапеций, расположенных над и под осью Ох, из которых составляется данная трапеция. Эту сумму и называют алгебраической площадью всей криволинейной трапеции.

Имея это в виду, мы в дальнейшем определенный интеграл всегда можем рассматривать независимо от конкретного смысла переменной интегрирования Х и функции как алгебраическУЮ площадь крИВолинейной трапеции с основанием , ограниченной линией .

В соответствии с этой геометрической иллюстрацией интеграла теорема IV (см. равенство (**)), выражающая свойство интеграла, которое называется Аддитивностью, означает тот наглядный факт, что если основание криволинейной трапеции разбить на частичные интервалы, то площадь всей трапеции будет равна сумме площадей трапеций, опирающихся на частичные интервалы.

< Предыдущая		Следующая >