20. Введение определенного интеграла
Некоторые задачи геометрии и физики. Как и к другим фундаментальным понятиям математики, к понятию
Интеграла приводят разнообразные вопросы других конкретных наук. Мы рассмотрим, прежде всего, такие важные задачи, как определение площади плоской фигуры и работы переменной силы. Разберем каждую из этих задач в отдельности.
I. Площадь криволинейной трапеции. Теория площадей исходит из двух положений:
1) Площадь фигуры, составленной из нескольких фигур, равна сумме площадей этих фигур;
2) Площадь прямоугольника равна произведению его измерений.
В элементарной геометрии, опираясь на эти положения, находят площадь треугольника, а также и площадь многоугольника, так как всякий многоугольник может быть разбит на треугольники. С помощью предельного перехода по площадям правильных вписанных и описанных многоугольников определяется площадь круга. Однако при этом используются особые геометрические свойства фигуры (круга), что в других случаях делается очень затруднительным.
Фигуру, площадь которой нужно определить, мы будем рассматривать в плоскости, снабженной системой декартовых координат.
Криволинейной трапецией будем называть фигуру, ограниченную осью Ох, линией, с которой любая прямая, параллельная оси Оу, пересекается не более чем в одной точке, и двумя прямыми х = а и х = b (рис. 1); интервал ![]() оси Ох назовем Основанием криволинейной трапеции.
оси Ох назовем Основанием криволинейной трапеции.
Обычно фигуру можно разбить на некоторое число криволинейных трапеций и, таким образом, искомую, площадь определить как алгебраическую сумму площадей криволинейных трапеций, составляющих эту фигуру. Так, например, площадь фигуры, изображенной на рис. 2, может быть представлена в виде следующей алгебраической суммы:
П. л. ![]() - п. л.
- п. л. ![]() + п. л.
+ п. л. ![]() - п. л.
- п. л. ![]()
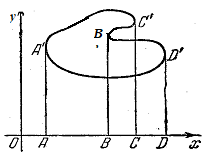
Отсюда следует, что для отыскания площади любой фигуры достаточно уметь находить площадь криволинейной трапеции.
Пусть криволинейная трапеция с основанием ![]() ограничена некоторой линией АВ, заданной уравнением
ограничена некоторой линией АВ, заданной уравнением ![]() , где
, где ![]() — непрерывная в интервале
— непрерывная в интервале ![]() функция.
функция.
Будем пока предполагать, что ![]() >0 в интервале
>0 в интервале ![]() , т. е. что трапеция расположена над осью Ох. Разделим основание трапеции — интервал
, т. е. что трапеция расположена над осью Ох. Разделим основание трапеции — интервал ![]() — На П частичных интервалов
— На П частичных интервалов ![]() посредством точек
посредством точек ![]()
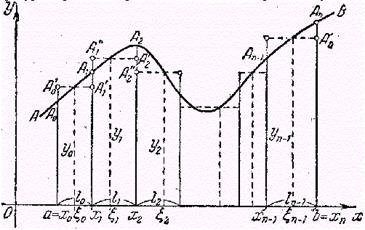
![]() (рис. 1). В этих частичных интервалах возьмем совершенно произвольные точки
(рис. 1). В этих частичных интервалах возьмем совершенно произвольные точки ![]() , так что
, так что ![]() . Рис. 2
. Рис. 2
Проведем ординаты ![]() линии АВ, соответствующие абсциссам
линии АВ, соответствующие абсциссам ![]() ; очевидно, мы имеем:
; очевидно, мы имеем:
![]()
На частичных интервалах ![]() как на основаниях построим П прямоугольников с высотами, равными соответственно ординатам
как на основаниях построим П прямоугольников с высотами, равными соответственно ординатам ![]() (рис. 1). Мы получили П-ступенчатую фигуру, которую также можно рассматривать как криволинейную трапецию с заданным основанием
(рис. 1). Мы получили П-ступенчатую фигуру, которую также можно рассматривать как криволинейную трапецию с заданным основанием ![]() , но ограниченную не заданной линией
, но ограниченную не заданной линией ![]() , а ломаной
, а ломаной ![]()
Площадь ![]() этой N-ступенчатой фигуры мы будем считать приближенным значением площади S заданной криволинейной трапеции, вообще говоря, тем более точным, чем больше П и чем меньше длИНы* ЧастичнЫх интервалов. Другими словами, мы исходим из того естественного и наглядного представления, что чем больше число прямоугольников и чем они УЖе, тем теснее построенная указанным сейчас способом ломаНАя линия
этой N-ступенчатой фигуры мы будем считать приближенным значением площади S заданной криволинейной трапеции, вообще говоря, тем более точным, чем больше П и чем меньше длИНы* ЧастичнЫх интервалов. Другими словами, мы исходим из того естественного и наглядного представления, что чем больше число прямоугольников и чем они УЖе, тем теснее построенная указанным сейчас способом ломаНАя линия ![]() примыкает к заданной линии
примыкает к заданной линии ![]() и тем лучше площадь
и тем лучше площадь ![]() соответствующеЙ N-ступенчатой Фигуры должна выражать площадь S заданной трапеции. Отсюда ясно, что Площадью S криволинейной трапеции, ограниченной ЛИнией
соответствующеЙ N-ступенчатой Фигуры должна выражать площадь S заданной трапеции. Отсюда ясно, что Площадью S криволинейной трапеции, ограниченной ЛИнией ![]() (рис. 1), Следует назвать предел, к которому стремится переменная площадь П-ступенчатой фигуры, ограниченной ломаной линией
(рис. 1), Следует назвать предел, к которому стремится переменная площадь П-ступенчатой фигуры, ограниченной ломаной линией ![]() , при неограниченном увеличении числа п и при стремлении к нулю наибольшей длины частичных интервалов.
, при неограниченном увеличении числа п и при стремлении к нулю наибольшей длины частичных интервалов.
Следует иметь в виду, что точки ![]() произвольны, но необходимо, чтобы при неограниченном увеличении числа П частичных интервалов длина наибольшего из них действительно стремилась к нулю. Если этого не предусмотреть, то может так случиться, что ступенчатая фигура не будет неограниченно приближаться к криволинейной трапеции. В самом деле, будем увеличивать число точек деления основания так, например, чтобы какой-нибудь частичный интервал, пусть
произвольны, но необходимо, чтобы при неограниченном увеличении числа П частичных интервалов длина наибольшего из них действительно стремилась к нулю. Если этого не предусмотреть, то может так случиться, что ступенчатая фигура не будет неограниченно приближаться к криволинейной трапеции. В самом деле, будем увеличивать число точек деления основания так, например, чтобы какой-нибудь частичный интервал, пусть ![]() (рис. 3), оставался неизменным. Тогда ломаная может неограниченно приближаться к дуге АС заданной линии
(рис. 3), оставался неизменным. Тогда ломаная может неограниченно приближаться к дуге АС заданной линии ![]() , но вовсе не будет приближаться к дуге СВ, и постоянная часть трапеции ССВB не будет при этом процессе покрываться нашими фигурами. Таким образом, по площадям этих фигур мы никак не сможем определить площадь трапеции. Если же указать, что длина наибольшего частичного интервала — обозначим ее через
, но вовсе не будет приближаться к дуге СВ, и постоянная часть трапеции ССВB не будет при этом процессе покрываться нашими фигурами. Таким образом, по площадям этих фигур мы никак не сможем определить площадь трапеции. Если же указать, что длина наибольшего частичного интервала — обозначим ее через ![]() — Стремится к нулю, то из этого следует, что число П частичных интервалов неограниченно возрастает.
— Стремится к нулю, то из этого следует, что число П частичных интервалов неограниченно возрастает.
Напишем теперь выражение для ![]() . Вся фигура состоит из П Прямоугольников, площадь каждого из которых выразить легко; именно площадь прямоугольника, соответствующего (I+1)-му частичному интервалу, очевидно, равна
. Вся фигура состоит из П Прямоугольников, площадь каждого из которых выразить легко; именно площадь прямоугольника, соответствующего (I+1)-му частичному интервалу, очевидно, равна ![]()
Значит,
![]() Или
Или
![]()
![]()
Все слагаемые этой суммы имеют один и тот же вид: отличаются они друг от друга только значениями индекса (указателя) При независимой переменной. Для сокращения записи вводят символ ![]() (греческая прописная буква «сигма») — символ суммы, именно пишут:
(греческая прописная буква «сигма») — символ суммы, именно пишут:
![]() (*)
(*)
Этот символ вообще означает, что нужно сложить выражения данного вида, придавая индексу все целые значения от значения, указанного под символом «сигма», до значения, указанного над символом «сигма».
В соответствии с определением площади S имеем:
![]()
Как указано выше, мы считаем, что переход к пределу совершается при условии ![]()
II. Работа переменной силы. Обратимся теперь к важной задаче физики — к определению работы. Мы увидим сейчас, что определение работы будет вполне аналогично определению площади трапеции.
Пусть под действием некоторой силы тело движется по прямой линии, причем направление силы совпадает с направлением движения. Требуется определить работу, произведенную при перемещения тела из положения М в положение N (рис. 4). Если на протяжении всего пути от М к N сила остается постоянной, то, как известно, работа определяется как произведение силы на длину пути. Обозначим через А работу, через Р — Силу, через S — длину пути MN. Тогда
A=PS.
Предположим, однако, что сила на пути от М к N изменяется. В каждой точке между М и N, находящейся на расстоянии S От точки М, действующая сила принимает сООтветствующее значение Р. Это значит, что сила Р есть некоторая функция расстояния S, т. Е. ![]() . Как определить работу, совершенную при перемещении тела из точки М в точку N в этом случае?
. Как определить работу, совершенную при перемещении тела из точки М в точку N в этом случае?
Разобьем весь путь MN, т. е. интервал изменения переменной S, на П участков точками, находящимися на расстояниях
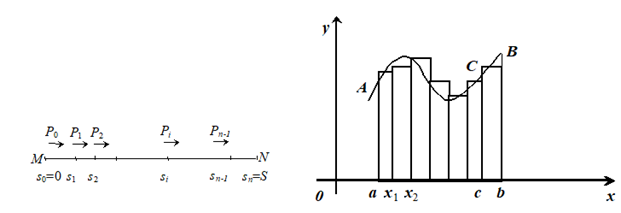
![]()
От точки М. Вместо действующей на пути MN переменной силы Р Возьмем другую силу РN, сохраняющую постоянные значения на каждом из наших участков, причем эти значения положим равными значениям действующей силы Р в каких-нибудь точках участков. На первом участке ![]() эта сила равна
эта сила равна ![]() , где
, где ![]() ; На втором
; На втором ![]() она равна
она равна ![]() , где
, где ![]() На (I+1)-м участке
На (I+1)-м участке ![]() оНА равна
оНА равна ![]() , где
, где ![]() и т. Д.
и т. Д.
Так как работа на всем пути равна сумме работ, соответствующих отдельным участкам, на которые разбит путь, то для работы ![]() , произведенной силой
, произведенной силой ![]() , будем, очевидно, иметь:
, будем, очевидно, иметь:
![]()
Величину ![]() мы полагаем приближенным значением искомой работы, вообще говоря, тем более точным, чем больше число П и чем меньше участки, на которые разбИВается весь путь MN. Работу A определяют как предел
мы полагаем приближенным значением искомой работы, вообще говоря, тем более точным, чем больше число П и чем меньше участки, на которые разбИВается весь путь MN. Работу A определяют как предел ![]() при
при ![]() ; при этом, как и раньше, предполагается, что длина наибольшего из частичных участков стремится к нулю:
; при этом, как и раньше, предполагается, что длина наибольшего из частичных участков стремится к нулю:
![]()
III. Путь. Скажем кратко еще об одной задаче физики - Об определении пути. Решение Этой задачи Будет произведено совершенно так же, как и предыдущих.
1) Предположим, что точка совершает поступательное движение, причем известна величина скорости V в любой момент времени T В некотором промежутке ![]() , т. е.
, т. е. ![]() .
.
Путь S, пройденный точкой за промежуток времени ![]() , Определяется так:
, Определяется так:
![]()
Где ![]() — Точки, разбивающие интервал
— Точки, разбивающие интервал ![]() На П частичных интервалов, причем
На П частичных интервалов, причем
![]()
![]()
Мы опять считаем, что ![]() . Каждое слагаемое
. Каждое слагаемое ![]() суммы дает путь, который прошло бы тело за промежуток времени
суммы дает путь, который прошло бы тело за промежуток времени ![]() , если бы оно двигалось в это время с постоянной скоростью, равной
, если бы оно двигалось в это время с постоянной скоростью, равной ![]() .
.
Определенный интеграл. Теорема Существования. В предыдущем пункте мы видели, что решение некоторых важных задач геометрии и физики (определение площади, работы, Пути) приводит к одной и той же последовательности действий над известными функциями и их аргументами. Раз эта последовательность действий применяется в различных случаях и имеет большое значение, то мы установим ее математически, независимо от конкретных условий той или иной задачи. Тогда и применение ее В каждом отдельном подходящем случае будет заранее узаконено и не будет требовать специальных рассуждений.
Если отвлечься от физического смысла переменных и От их обозначений, то указанная последовательность действий состоит в следующем:
1) интервал ![]() , в котором задана непрерывная функция
, в котором задана непрерывная функция ![]() (теперь мы отбросим предположение, что
(теперь мы отбросим предположение, что ![]() в интервале
в интервале ![]() ), Разбивается на N частичных интервалов при помощи точек
), Разбивается на N частичных интервалов при помощи точек ![]() , причем
, причем ![]()
2) значение функции ![]() в какой-нибудь точке
в какой-нибудь точке ![]() -го частичного интервала
-го частичного интервала ![]() умножается на длину этого интервала
умножается на длину этого интервала ![]() , т. Е. составляется произведение
, т. Е. составляется произведение ![]() ;
;
3) берется сумма ![]() всех этих произведений
всех этих произведений
![]()
Или, если обозначить ![]() через
через ![]() ,
,
![]() (А)
(А)
4) находится предел I суммы ![]() при стремлении к нулю длины наибольшего частичного интервала, и следовательно, при
при стремлении к нулю длины наибольшего частичного интервала, и следовательно, при ![]() ,т. е.
,т. е.
![]()
В рассмотренных выше четырех конкретных задачах этот предел I измеряет соответственно площадь, работу, путь. В общем случае он называется Определенным ИНтегралом или просто Интегралом от функции ![]() в пределах от А до B и обозначается так:
в пределах от А до B и обозначается так:
![]()
И читается: интеграл от А до B ![]() На Dx. Следовательно, по определению
На Dx. Следовательно, по определению
 (*)
(*)
Сумма (А) называется П-й ИНтегральной суммой.
ОпредеЛЕние. Определенным интегралом называется Предел, к которому стремится П-я интегральная сумма (А) прИ стремлении к нулю длины наибольшего ЧАстичного интервала.
Применяя ОпределенИе иНТеграла к четырем конкретным вопросам, разобранным вЫше пОЛУченнЫЕ выводы выразить в таких словах:
1) ПЛОщадь крИВолинейной трапеции равна интегралу от Ординаты линии, ограничиваюЩЕй трапецию, взятому по основанию: ![]() ;
;
2) работа, Произведенная силой, равна интегралУ от силы, взятому по пути:
![]()
3) Путь, пройденный телом, равен интегралу от скорости, взятому по времени:
Имеет место следующая так называемая теорема существованИЯ определенного интеграла:
Теорема, П-я иНТегральНАя сумма, соответствующая Конечному Иитервалу ![]() изменения переменНОй Х,
изменения переменНОй Х, ![]() , и неПрЕрывной на нем фуНКции
, и неПрЕрывной на нем фуНКции ![]() , при стремлеНИи к нулю длины наибольшего частичного интервала стремится к пределу, и притом к одному и тому же, независимо от способа разбиенИЯ интервала
, при стремлеНИи к нулю длины наибольшего частичного интервала стремится к пределу, и притом к одному и тому же, независимо от способа разбиенИЯ интервала ![]() на частичные интервалы
на частичные интервалы ![]() и независимо от того, какие значения Х в частичных интервалах
и независимо от того, какие значения Х в частичных интервалах ![]() принимаются в качестве чисел
принимаются в качестве чисел ![]() .
.
Доказывать теорему мы не будем.
Символ интеграла указывает на его происхождение: ![]() Является как бы вытянутой буквой S, первой буквой слова «Summa»; выражение, стоящее справа от (говорят также: ПОД) символа интеграла, показывает вид суммируемых слагаемых; индекс при переменной в выражении под интегралом опущен, чем подчеркивается, что в процессе суммирования, завершающегося предельным переходом, переменная Х Принимает все значения в интервале
Является как бы вытянутой буквой S, первой буквой слова «Summa»; выражение, стоящее справа от (говорят также: ПОД) символа интеграла, показывает вид суммируемых слагаемых; индекс при переменной в выражении под интегралом опущен, чем подчеркивается, что в процессе суммирования, завершающегося предельным переходом, переменная Х Принимает все значения в интервале ![]() ; числа, стоящие под и над символом интеграла, указывают концы интервала, на котором производилось суммирование.
; числа, стоящие под и над символом интеграла, указывают концы интервала, на котором производилось суммирование.
Функция ![]() называется Подынтегральной функцией, выражение
называется Подынтегральной функцией, выражение ![]() — подынтегральным выражением, число А — нижнИМ, а число B — верхним пределами интеграла, переменная Х -— переменноЙ интегрирования, интервал
— подынтегральным выражением, число А — нижнИМ, а число B — верхним пределами интеграла, переменная Х -— переменноЙ интегрирования, интервал ![]() — интервалом интегрирования. Интегральные суммы, составленные при различных разбиениях интервала интегрирования и различных выборах точек
— интервалом интегрирования. Интегральные суммы, составленные при различных разбиениях интервала интегрирования и различных выборах точек ![]() , могут отличаться друг от друга весьма значительно. Сформулированная Выше Замечательная теорема показывает, что разница между ними стирается, вообще говоря, по мере возрастания числа точек деления и убывания длины наибольшего частичного интервала, совсем ИСчезая в пределе.
, могут отличаться друг от друга весьма значительно. Сформулированная Выше Замечательная теорема показывает, что разница между ними стирается, вообще говоря, по мере возрастания числа точек деления и убывания длины наибольшего частичного интервала, совсем ИСчезая в пределе.
Символ ![]() изображает просто число. Это число не зависит от обозначения переменной интегрирования, так что справедливо равенство
изображает просто число. Это число не зависит от обозначения переменной интегрирования, так что справедливо равенство ![]()
Операция вычисления определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования называется Определенным интегрированием функцИЙ.
Вычисление определенного интеграла при помощи метода, прямо вытекающего из определения, встречает трудности в самых, казалось бы, простых случаях. Поэтому мы даже не будем приводить примеров такого вычисления и прямо перейдем к изложению основных свойств определенного интеграла, которые, в конечном счете, и приведут нас к установлению обходного, несравненно более удобного и легкого пути для вычисления интегралов.
| < Предыдущая | Следующая > |
|---|