15. Закрытая и открытая модели транспортной задачи
Модель ТЗ называют закрытой (сбалансированной), если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т. е. выполняется равенство:
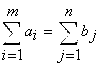 .
.
Если для транспортной задачи выполняется одно из условий:
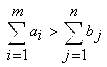 , (3.3)
, (3.3)
 , (3.4)
, (3.4)
То модель задачи называют Открытой (несбалансированной).
Для разрешимости ТЗ с открытой моделью необходимо преобразовать ее в закрытую модель.
Так, при выполнении условия (3.3) необходимо ввести фиктивный (n+1)-й пункт назначения ![]() , т. е. в матрице задачи добавляется столбец. Спрос фиктивного потребителя полагают равным небалансу, т. е.
, т. е. в матрице задачи добавляется столбец. Спрос фиктивного потребителя полагают равным небалансу, т. е.  , а стоимость перевозок равной нулю, т. е.
, а стоимость перевозок равной нулю, т. е. ![]() . Переменные
. Переменные ![]() – это количество груза, которое останется в I-ом пункте отправления. Аналогично при выполнении условия (3.4) вводится фиктивный поставщик
– это количество груза, которое останется в I-ом пункте отправления. Аналогично при выполнении условия (3.4) вводится фиктивный поставщик ![]() , т. е. в матрице задачи добавляется строка. Запас груза фиктивного поставщика равен
, т. е. в матрице задачи добавляется строка. Запас груза фиктивного поставщика равен ![]() , а тарифы (стоимости перевозок) равны нулю, т. е.
, а тарифы (стоимости перевозок) равны нулю, т. е. ![]() . Переменные
. Переменные ![]() – это количество груза, недостающее J-му пункту назначения.
– это количество груза, недостающее J-му пункту назначения.
При преобразовании открытой модели задачи в закрытую модель целевая функция не изменяется, так как все слагаемые, соответствующие дополнительным перевозкам, равны нулю.
Целевая функция (3.1) и система ограничений (3.2) являются экономико-математической моделью сбалансированной ТЗ.
Алгоритм решения сбалансированной транспортной задачи
1 Строим исходный опорный план.
2 Проверяем его на оптимальность. Если план оптимален, задача решена. Иначе переходим к пункту 3.
3 Переходим к нехудшему опорному плану. Возвращаемся к пункту 2.
| < Предыдущая | Следующая > |
|---|