14. Постановка транспортной задачи по критерию стоимости в матричной форме

В m пунктах отправления сосредоточен однородный груз в количестве соответственно единиц. Имеющийся груз необходимо доставить потребителям , спрос которых выражается величинами единиц. Известна стоимость перевозки единицы груза из -го () пункта отправления в -й () пункт назначения.

Требуется составить план перевозок, который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимизируются.

Для наглядности условие транспортной задачи (ТЗ) можно представить таблицей, которую будем называть Распределительной. Распределительную таблицу называют иногда табличной или Матричной моделью ТЗ (см. таблицу 14).

Таблица 14

Поставщик	Потребитель	Запас груза,
			...
			...
			...
...	...	...	...	...
			...
Потребность В грузе			...

Для построения экономико-математической модели ТЗ введем переменные – количество груза, которое необходимо доставить из -го пункта отправления в -й пункт назначения.

Матрицу 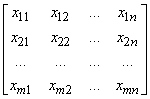будем называть Матрицей перевозок.

Цель ТЗ – минимизировать общие затраты на реализацию плана перевозок. Следовательно, целевая функция будет иметь вид

(3.1)

Составим систему ограничений, которая будет определять ОДР данной задачи в случае, когда .

Первые m уравнений системы (3.2) – это ограничения на запас груза у поставщиков, следующие n уравнений системы (3.2) – это ограничения на потребности потребителей в грузе, неравенства системы – это ограничения на смысл переменных (количество груза не может быть отрицательным).

(3.2)

Будем называть план перевозок

Допустимым, если он удовлетворяет системе ограничений (3.2).

Допустимый план перевозок, доставляющий минимум целевой функции, называется Оптимальным.

< Предыдущая		Следующая >