38. Дифференциальные операции второго порядка. Лапласово (гармоническое) векторное поле
Дифференциальные операции второго порядка – это повторно примененные операции grad, div и rot к скалярным и векторным полям, полученным в результате применения этих же операций к скалярным ![]() и векторным
и векторным ![]() полям. Возможны лишь следующие повторные операции:
полям. Возможны лишь следующие повторные операции: ![]() ;
; ![]() ,
,
где  - лапласиан;
- лапласиан; ![]() ;
; ![]() ;
; ![]()
![]() .
.
Операции первого и второго порядков удобно записывать (и вычислять, доказывать) с помощью специального символического оператора ![]() (читается “набла”):
(читается “набла”):
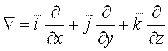 . (2.9)
. (2.9)
Для дифференциальных операций первого порядка имеем
![]() ;
; ![]()
![]() . (2.10)
. (2.10)
Операции второго порядка:
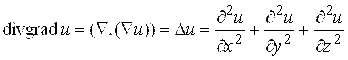 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
При применении оператора “набла” руководствуются следующим правилом: при применении оператора ![]() к произведениям скалярных
к произведениям скалярных ![]() ,
, ![]() ) и векторных
) и векторных ![]() ,
, ![]() полей:
полей: ![]() можно поступать так: применить оператор
можно поступать так: применить оператор ![]() к каждому из сомножителей отдельно, считая другой постоянным (их обозначаем
к каждому из сомножителей отдельно, считая другой постоянным (их обозначаем ![]() ), и результаты сложить; затем каждоеслагаемое преобразовать по правилам векторной алгебра так, чтобы оператор
), и результаты сложить; затем каждоеслагаемое преобразовать по правилам векторной алгебра так, чтобы оператор![]() стоял на предпоследнем месте перед переменным множителем.
стоял на предпоследнем месте перед переменным множителем.
Пример. Показать, что ![]() .
.
Решение. В символической форме записи ![]() . Учитывая сначала дифференциальный характер
. Учитывая сначала дифференциальный характер ![]() , мы должны написать
, мы должны написать ![]() . Рассматривая выражение
. Рассматривая выражение ![]() мы можем постоянный множитель
мы можем постоянный множитель ![]() вынести за знак “набла” и, как скаляр, за знак скалярного
вынести за знак “набла” и, как скаляр, за знак скалярного
произведения, что дает ![]() (на последнем шаге мы опустили индекс “C”).
(на последнем шаге мы опустили индекс “C”).
В выражении ![]() оператор
оператор ![]() действует только на скалярную функцию U; поэтому мы можем написать, что
действует только на скалярную функцию U; поэтому мы можем написать, что ![]() . В результате получаем формулу
. В результате получаем формулу ![]() или
или ![]() .
.
Задачи для самостоятельного решения
Найти потенциалы следующих плоских и трехмерных полей:
91. ![]() ; 92.
; 92. 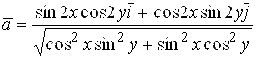 ;
;
93. ![]() ; 94.
; 94. ![]() ;
;
95. ![]() ; 96.
; 96. 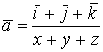 ; 97.
; 97.  ;
;
98. ![]() ; 99.
; 99. 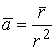 ; 100.
; 100. ![]() ;
;
101.  ;
;
102.  ;
;
103.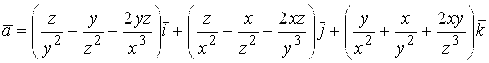 .
.
104. Доказать, что поле вихрей соленоидально: ![]() .
.
105. Доказать, что в соленоидальном поле поток вектора через замкнутую поверхность, не содержащую внутри особых точек, равен нулю.
В задачах 106 – 109 проверить соленоидальность заданных полей:
106. ![]() ; 107.
; 107. ![]() ;
;
108.  ; 109.
; 109.  .
.
110. Доказать, что в соленоидальном поле поток вектора поля через поперечное сечение любой векторной трубки (определенный в одном и том же направлении) сохраняет постоянное значение.
111. Показать, что поле вектора  соленоидально во всякой области, не содержащей начало координат O(0,0,0).
соленоидально во всякой области, не содержащей начало координат O(0,0,0).
112. Найти условие соленоидальности поля ![]() .
.
113. Показать, что в соленоидальном поле поток вектора ![]() не зависит от вида поверхности (S), натянутой на данный контур (L), а зависит только от самого контура.
не зависит от вида поверхности (S), натянутой на данный контур (L), а зависит только от самого контура.
114.Показать, что векторное поле ![]() - соленоидальное и безвихревое.
- соленоидальное и безвихревое.
Используя правило применения оператора ![]() к произведениям скалярных и векторных полей, доказать справедливость следующих формул:
к произведениям скалярных и векторных полей, доказать справедливость следующих формул:
115. ![]() ; 116.
; 116. ![]() ;
;
117.![]() ; 118.
; 118.![]() ;
;
119. ![]() ;
;
120. ![]() ;
;
121. ![]() .
.
122. Найти ![]() . В каком случае
. В каком случае ![]() ?
?
123. Показать, что скалярное поле ![]() ,
, ![]() , является гармоническим
, является гармоническим ![]() .
.
В задачах 124 – 131 выяснить, какие поля – гармонические, какие – нет:
124.  125.
125. ![]() 126.
126. ![]()
127. ![]() 128.
128. ![]()
129.![]()
130. ![]()
131. ![]()
![]()
132. Найти все гармонические поля, зависящие только от X.
133. Найти общий вид однородного гармонического многочлена второй степени от X и Y.
134. Найти все решения уравнения Пуассона ![]() , зависящие только от X.
, зависящие только от X.
Ответы к задачам главы 15
1. ![]() 2.
2.![]() 3.
3. ![]() 4.
4. . 5.
. 5.![]() 6.
6. 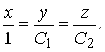
7.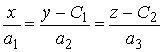 . 8.
. 8. ![]() 9.
9. ![]()
10. ![]() 11.
11. ![]()
12. ![]() 13.
13.  . 14.
. 14. 
15. ![]() 16.
16. ![]() 17.
17. ![]() 18.
18. ![]() 19.
19. ![]() 20.0. 21.
20.0. 21. ![]() 22. 0,25. 23.
22. 0,25. 23. ![]() 24.
24. ![]() 25.
25. ![]() 26.
26. ![]() 27.
27. ![]() 28.
28. ![]()
29. ![]() 30.
30. ![]() 31.
31. ![]() 32.
32. ![]() 33.
33. ![]() 34.
34. ![]() 35.0.
35.0.
36. ![]() 37. а) 2/3; б) 0,7; в) 0,7; г)1; д) 1. 38.
37. а) 2/3; б) 0,7; в) 0,7; г)1; д) 1. 38. ![]() 39.
39. ![]() 40.
40. ![]()
41. ![]() 42.
42. ![]() 43.
43. ![]() 44.
44. ![]() 45.
45. ![]() 46. –14. 47.
46. –14. 47. ![]() 48.
48. 49.
49. ![]() 50.
50. 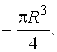 51. 4/3. 52.
51. 4/3. 52. ![]() 53.
53. ![]() . 54.
. 54. ![]()
55. ![]() 56. 0. 57. 0. 58.
56. 0. 57. 0. 58. ![]() 59. 0. 60. 1. 61.
59. 0. 60. 1. 61. ![]() 62.
62. ![]() 63.
63. ![]()
64. 0. 65. ![]() 66.
66. ![]() 67.
67.![]() 68.
68. ![]() 69.
69. ![]() 70.
70. ![]() 71.-1. 72.
71.-1. 72.![]() 73.
73. ![]() 74.
74. ![]() 81.
81. ![]()
![]() 82.
82. ![]() 83.
83.![]() 84.
84. ![]() 85.
85.![]() 86.
86. ![]() 87.
87. ![]() 88. 0.
88. 0.
89. ![]() 90.
90.![]() 91.
91. ![]() 92.
92. ![]() 93.
93. ![]() 94.
94.![]() 95.
95. ![]() 96.
96. ![]() 97.
97. ![]() 98. R. 99. LnR. 100.
98. R. 99. LnR. 100. ![]() . 101.
. 101.  102.
102. 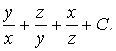
103. 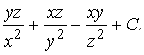 112.
112. ![]()
![]() C=const. 122.
C=const. 122.![]()
![]() 124. Нет. 125. Нет. 126. Да. 127. Только при A+C=0.
124. Нет. 125. Нет. 126. Да. 127. Только при A+C=0.
128. Только, если A+C=B+D=0. 129. Да. 130. Только при ![]()
131. Только если ![]()
![]() .
.
132. ![]() 133.
133. ![]() A и B – любые.
A и B – любые.
134. 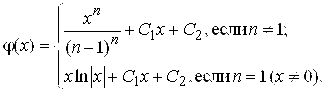
| < Предыдущая |
|---|