31. Поток векторного поля. Определение потока векторного поля

Рассмотрим векторное поле , где проекции - непрерывные функции в некоторой области (V). Возьмем некоторую гладкую (кусочно гладкую) двустороннюю ориентированную поверхность (S) (то есть двустороннюю поверхность с выбранным на ней направлением нормали).

Определение. Потоком П векторного поля через двустороннюю ориентированную поверхность (S) называется поверхностный интеграл первого рода по поверхности (S):

. (1.3)

Здесь - орт нормали к выбранной стороне (S); Ds – элемент площади поверхности (S).

Замечание. В случае замкнутой поверхности ее ориентируют, направляя нормаль изнутри области (V) наружу. Сторона с положительным направлением нормали называется положительной стороной поверхности.

Для потока можно дать следующие записи через поверхностные интегралы первого и второго рода :

(1.3¢)

Где , , - то есть - проекции площадки на плоскости Oyz, Oxz, Oxy соответственно.

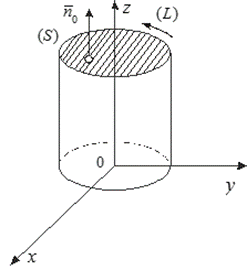
Пример. Вычислить поток векторного поля - радиус-вектор точки ) через полную поверхность прямого кругового цилиндра с высотой H и радиусом основания R (см. рис.1).

Рис.1.

Решение. Так как поверхность (S) есть объединение поверхностей и , то поэтому для потока П (по свойству аддитивности) имеем: . На боковой поверхности нормаль параллельна плоскости Oxy; следовательно, и поток =. На нижнем основании нормаль Параллельна оси Oz: . Тогда и ; на стороне нормаль И , т. е. и .Искомый поток . Обратим внимание на то, что . Ниже увидим, что это не случайно.

< Предыдущая		Следующая >