3.3. Достаточные признаки равномерной сходимости функциональных рядов

Определение: Числовой ряд называется мажорантным (или мажорирующим) для функционального ряда на множестве X, если .

Пример 2: ; ; .

Теорема 2 (Признак Вейерштрасса):

Если для функционального ряда на множестве Х существует мажорантный сходящийся ряд , то исходный функциональный ряд сходится на множестве Х.

Док-во: Зададим произвольное , по критерию Коши для числовых рядов И – натурального, выполняется условие 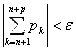. Т. к. по условию , то – натурального и выполняется 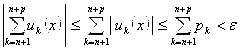. Таким образом, для функционального ряда выполняется критерий Коши равномерной сходимости, ч. т.д.

Признак Дирихле-Абеля

Определение: Функциональная последовательность называется равномерно ограниченной

На множестве Х, если существует константа M такая, что .

Пример 3: Функциональная последовательность является равномерно ограниченной на множестве выполняется .

Признак Дирихле-Абеля относится к рядам следующего фиксированного вида:

Теорема 3 (признак Дирихле-Абеля равномерной сходимости функциональных последовательностей):

Пусть:

Функциональная последовательность не возрастает при каждом а сходится к нулю равномерно на множестве Х (т. е. на X). Последовательность равномерно ограничена на множестве X. Тогда ряд сходится равномерно на множестве X.

Док-во: Признака Дирихле-Абеля полностью повторяет схематично доказательство данного признака для числовых рядов.

Пример 4: . Будем считать, что ( не зависит от X). Причем последовательность является убывающей последовательностью, потому выполнено условие (1) признака Дирихле-Абеля: выполним следующую оценку: при .

Рассмотрим сколь угодно малое выполняется, что , следовательно, выполнено условие (2) признака Дирихле-Абеля, а значит, по Теореме 3 исходный ряд сходится на .

< Предыдущая		Следующая >