2.1. Скалярные и векторные поля

1. Скалярное поле

Если каждой точке (на плоскости или в пространстве) поставлено в соответствие некоторое число , то говорят, что в области G задано скалярное поле. Скалярное поле зависит от выбора точки M и не зависит от выбора прямоугольной системы координат. В этом случае можно говорить, что фиксирована некоторая функция , где , задаем скалярное поле в области G.

2. Векторное поле

Если каждой точке поставлен в соответствие некоторый вектор , то говорят, что в области G задано векторное поле. Векторное поле зависит от выбора точки M и не зависит от выбора прямоугольной системы координат. При фиксированной декартовой системе координат векторное поле может быть задано вектором или тремя скалярными функциями P(X,Y,Z), Q(X,Y,Z), R(X,Y,Z):

Определение: Кривая L называется векторной линией векторного поля , если в каждой точке данной кривой, вектор, задающий векторное поле, является касательным вектором к данной кривой.

3. Градиент и производная по направлению

Здесь и в дальнейшем будем полагать, что функции, задающие скалярные и векторные поля имеют непрерывные частные производные первого порядка.

Данное определение градиента связано с выбором системы координат, но на самом деле вектор grad U не зависит от выбора системы координат, поскольку его направление указывает на направление наибольшего роста скалярной величины U, а его длина равна скорости роста величины U вдоль этого направления.

4. Дивергенция

Определение: Дивергенцией векторного поля является скалярная функция:

,

Где P, Q, R – компоненты вектора .

Данное определение дивергенции связано с выбором системы координат; далее будет показано, что не зависит от системы координат.

5. Ротор (вихрь)

Определение: Ротором векторного поля называется вектор-функция

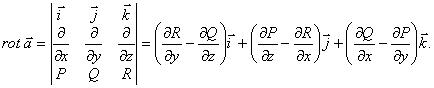
Будет показано, что ротор тоже не зависит от системы координат.

6. Циркуляция

Пусть в области G задано векторное поле и пусть AB – кривая, целиком лежащая в области G. Рассмотрим следующий интеграл:

Такой интеграл называется циркуляцией вдоль векторного поля вдоль кривой AB.

7. Поток

Пусть в области G задано векторное поле . Пусть P – гладкая, двусторонняя поверхность, лежащая в области G. Выберем одну из сторон поверхности и зафиксируем непрерывное поле нормалей .

Определение: Поверхностный интеграл второго рода по выбранной стороне поверхности

Называется потоком векторного поля через ориентированную поверхность P. Поток векторного поля не зависит от выбора системы координат.

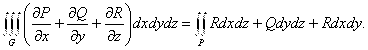
8. Инвариантное определение дивергенции

Введем вектор , тогда формула Остроградского-Гаусса может быть переписана в следующем приемлемом виде:

Рассмотрим произвольную точку M и окружим эту точки гладкой поверхностью P, которая ограничивает область G, где находится точка M. Обратимся к формуле Остроградского-Гаусса и применим для нее формулу среднего значения, то есть для некоторой точки M* (такая точка найдется), справедливо следующее равенство:

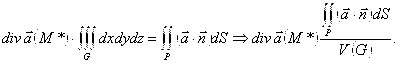
Будем теперь стягивать поверхность P к точке M, так, что, а . В пределе получим следующее равенство:

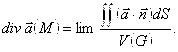
Полученная формула показывает, что поток векторного поля и объем не зависят от выбора системы координат и, следовательно, не зависит от выбора системы координат, а зависит только от самого векторного поля .

9. Инвариантное определение ротора

Теперь воспользуемся формулой Стокса:

Введем вектор , тогда формула Стокса переписывается в следующем виде:

Рассмотрим произвольную точку M, проведем через точку M плоскость и окружим точку M некоторым замкнутым контуром L, лежащим в этой плоскости. Запишем для поверхности P формулу Стокса и запишем формулу среднего значения:

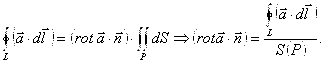
Так как циркуляция векторного поля и не зависит от выбора системы координат, то проекция вектора на произвольное направление n не зависит от выбора системы координат, а значит и сам вектор не зависит от выбора системы координат.

Теорема 1 (о независимости криволинейного интеграла второго рода от пути интегрирования)

Пусть:

1. Функции P(X,Y,Z), Q(X,Y,Z), R(X,Y,Z) определены и непрерывны в области G , тогда следующие три условия являются эквивалентными (т. е. из каждого условия следуют два других):

1) Для любого замкнутого контура LÎG; .

2) Для любых двух точек A, BÎG Не зависит от пути интегрирования

3) Является полным дифференциалом, т. е.$ U=U(X,Y,Z), такая, что

.

При этом выполняется .

2. Если, кроме того, область G является поверхностно односвязной областью, а функции P, Q и R имеют области G непрерывные частные производные первого порядка, то каждое из условий 1-3 эквивалентно последующему условию.

< Предыдущая		Следующая >