29. Метод Рунге – Кутты решения дифференциального уравнения, Методы Эйлера

Методы Рунге - Кутты обладают следующими отличительными свойствами:

1) являются одношаговыми: чтобы найти нужна информация только о предыдущей точке ;

2) согласуются с рядом Тейлора вплоть до членов порядка , где степень различна для различных методов и называется порядком метода;

3) не требуют вычисления производных от , а только вычисления функции.

Именно благодаря третьему свойству методы Рунге - Кутты более известны, нежели ряд Тейлора. Однако для вычисления одной последующей точки решения приходится вычислять несколько раз при различных значениях

Выведем сначала некоторые формулы на основе геометрических аналогий.

Пусть известна точка на искомой кривой. Через эту точку можно провести прямую с тангенсом угла наклона

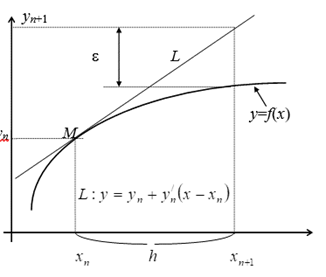
Тогда следующей можно считать точку, где прямая пересечет ординату, проведенную через точку Уравнение прямой имеет вид но так как , то (7.4.1)

Формула (7.4.1) описывает метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Формула (7.4.1) может быть получена из (7.2.2), если принять . Так как здесь функция не зависит от , то метод является явным.

Ошибка интегрирования при показана на рисунке в виде отрезка . Очевидно, что найденное таким образом приближенное решение согласуется с разложением в ряд Тейлора вплоть до членов порядка , так что ошибка равна

Теорема 7.2. Пусть функция Удовлетворяет условию Тогда справедливо неравенство

(7.4.2)

То есть метод Эйлера устойчив на конечном отрезке. Здесь - погрешность аппроксимации дискретного уравнения (7.2.1) на решении .

< Предыдущая		Следующая >