27. Сходимость метода Ньютона и трудности его применения

Теорема 6.1. Пусть - Простой корень уравнения , в некоторой окрестности которого функция Дважды непрерывно дифференцируема. Тогда найдется такая малая -окрестность корня , что при произвольном выборе начального приближения из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы этой окрестности и справедлива оценка

(6.3.1)

Где . Это означает, что метод Ньютона сходится с квадратичной скоростью. Грубо говоря, на каждой итерации число верных знаков приближения примерно удваивается.

Простота и высокая скорость сходимости делает метод Ньютона чрезвычайно привлекательным.

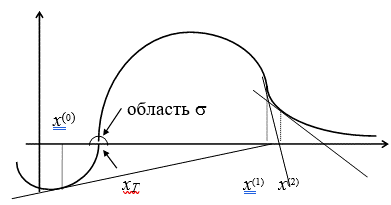
Однако имеются две существенные трудности. Первая из них - необходимость вычисления производной Это часто либо невозможно сделать, либо вычисление оказывается слишком дорогим. В таких ситуациях прибегают к различным модификациям метода Ньютона. Вторая трудность - его локальная сходимость. Это значит, что последовательные приближения сходятся к точному решению лишь в малой -Окрестности точки . Неудачный выбор начального приближения может дать расходящуюся последовательность (см. рисунок слева). Для преодоления этой трудности часто на практике используют метод Ньютона в сочетании с каким-нибудь медленно, но гарантированно сходящимся методом типа метода бисекции.

< Предыдущая		Следующая >