25. Решение нелинейных уравнений

Пусть дано уравнение Корнем этого уравнения называется такое значение , при котором Корень называется простым, если , в против-
ном случае - кратным. Целое число называется кратностью корня , если

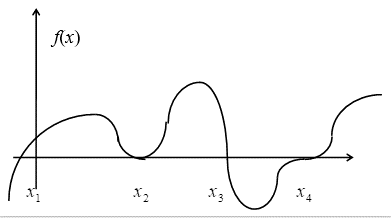
Геометрически корень соответствует точке пересечения графика функции с осью Корень кратный, когда пересечение происходит под нулевым углом. На рисунке , - простые корни, , - кратные. В подавляющем большинстве случаев представить решение уравнения в виде конечной замкнутой формулы оказывается невозможным. Даже для простейшего алгебраического уравнения -й степени явные формулы корней известны для Уже для уравнения пятой (и более высоких степеней) таких формул не существует.

Задача отыскания корней нелинейного уравнения решается в два этапа. Первый называется этапом локализации (отделения) корней, второй - этапом итерационного уточнения корней. Отрезок , содержащий только один корень уравнения , называется отрезком локализации корня . Способы локализации корней многообразны, и указать универсальный метод не представляется возможным. Иногда отрезок локализации известен либо он определяется из физических соображений. В простых случаях хороший результат может дать графический метод. На этапе итерационного уточнения корней с точностью используют тот или иной итерационный метод, позволяющий строить последовательность приближений к корню . Итерационный метод называют одношаговым, если для вычисления очередного приближения используется только одно предыдущее приближение и - шаговым, если для вычисления используется предыдущих приближений Столько же данных необходимо для начального приближения, чтобы запустить метод.

Скорость сходимости - одна из важнейших характеристик итерационных методов. Говорят, что метод сходится со скоростью геометрической прогрессии, знаменатель которой , если для справедлива оценка:

(6.1.1)

При определении скорости сходимости метода используют понятие порядка сходимости. Если справедливо неравенство

(6.1.2)

То число Называют порядком сходимости. Если , то сходимость линейная (сходимость геометрической прогрессии), при сходимость называется сверхлинейной. Если , скорость сходимости называют квадратичной.

Если , то есть метод обладает линейной сходимостью, можно установить справедливость формулы

; (6.1.3)

Смотрите метод простых итераций или метод Зейделя в предыдущей главе. Если же , то справедлива оценка

(6.1.4)

< Предыдущая		Следующая >