22. Метод простых итераций. Сходимость метода итераций
Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невозможно из-за ограничений технического характера. Большие системы уравнений, возникающие в приложениях, как правило, являются разреженными. При использовании метода Гаусса, например, большое число нулевых элементов превращаются в ненулевые и матрица теряет свойство разреженности. Использование итерационных методов не меняет матрицу коэффициентов, она остается разреженной.
Однако применение итерационных методов для качественного решения требует серьезного использования структуры системы уравнений, специальных знаний и опыта.
Пусть дана система ![]() - квадратная невырожденная матрица. Преобразуем ее к виду
- квадратная невырожденная матрица. Преобразуем ее к виду ![]() (5.5.1)
(5.5.1)
Где ![]() - квадратная матрица такой же размерности что и
- квадратная матрица такой же размерности что и ![]() ,
, ![]() - вектор - столбец. В развернутой форме записи система (5.5.1) имеет вид
- вектор - столбец. В развернутой форме записи система (5.5.1) имеет вид
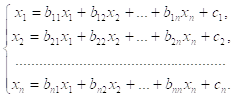 (5.5.2)
(5.5.2)
Операция приведения системы ![]() к виду (5.5.2) не является очевидной и простой и требует специальных знаний, а также существенного использования специфики системы. Самый простой способ приведения системы
к виду (5.5.2) не является очевидной и простой и требует специальных знаний, а также существенного использования специфики системы. Самый простой способ приведения системы ![]() к виду (5.5.2) состоит в последовательном исключении из первого уравнения системы
к виду (5.5.2) состоит в последовательном исключении из первого уравнения системы ![]() переменной
переменной ![]() , из второго уравне-
, из второго уравне-
ния - переменной ![]() и так далее. Метод итерации в такой реализации называется методом Якоби. Система уравнений метода Якоби имеет вид
и так далее. Метод итерации в такой реализации называется методом Якоби. Система уравнений метода Якоби имеет вид
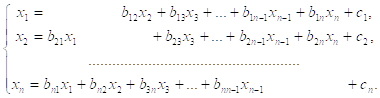 (5.5.3)
(5.5.3)
На главной диагонали матрицы ![]() системы (5.5.3) стоят нули, а остальные элементы, очевидно, выражаются по формулам
системы (5.5.3) стоят нули, а остальные элементы, очевидно, выражаются по формулам ![]()
Практически метод работает следующим способом. Выбирается начальное приближение ![]() и подставляется в правую часть системы (5.5.1). Решая систему, находят первое приближение
и подставляется в правую часть системы (5.5.1). Решая систему, находят первое приближение ![]() Это приближение опять подставляют в правую часть (5.5.1). Таким образом, получается
Это приближение опять подставляют в правую часть (5.5.1). Таким образом, получается ![]() Продолжая этот процесс далее, получим последовательность
Продолжая этот процесс далее, получим последовательность ![]() приближений, вычисляемых по формуле
приближений, вычисляемых по формуле
![]() (5.5.4)
(5.5.4)
В развернутой форме записи система (5.5.4) выглядит таким образом:
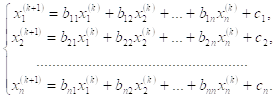 (5.5.5)
(5.5.5)
| < Предыдущая | Следующая > |
|---|