21. Метод Гаусса решения систем линейных алгебраических уравнений

Вычисления с помощью метода Гаусса состоят из двух основных этапов, называемых прямым и обратным ходом. Прямой ход заключается в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных происходят на этапе обратного хода. Прямой ход состоит из шагов.

1-й шаг. Целью этого шага является исключение неизвестного из уравнений с номерами Пусть Тогда этот элемент называется главным (ведущим) элементом первого шага. Найдем Вычтем последовательно из второго, третьего,..., -го уравнения системы (5.1.1) первое уравнение, умноженное соответственно на Это позволит обратить в нуль коэффициенты при во всех уравнениях, кроме первого. В результате будет получена эквивалентная система (5.3.1), в которой :

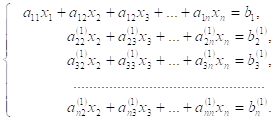(5.3.1)

2-й шаг. Целью этого шага является исключение неизвестного из уравнений с номерами Пусть - ведущий элемент второго шага; положим опять и вычтем из третьего, четвертого,..., -го уравнений второе уравнение, умноженное на соответственно. Получим

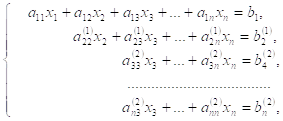(5.3.2)

Где В результате после -го шага исключения получим следующую треугольную систему уравнений:

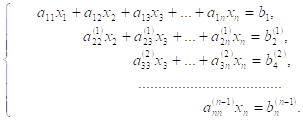(5.3.3)

На этом вычисления прямого хода заканчиваются.

Обратный ход посвящен нахождению неизвестных Из последнего уравнения системы (5.3.3) находим сразу Подставляя найденное значение в предпоследнее уравнение, получим Осуществляя обратную подстановку, далее последовательно находим

Общее число арифметических операций прямого хода в методе Гаусса примерно , обратного - всего около , что при большом пренебрежимо мало по сравнению с числом операций прямого хода.

Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы Поэтому если один из главных элементов оказывается близким к нулю, то схема единственного деления в уже описанном виде не может быть реализована. В этом случае прибегают к выбору главного элемента по столбцу (схема частичного выбора) или в выбору главного элемента по всей матрице (схема полного выбора).

В схеме частичного выбора главного элемента на каждом -м шаге исключения выбирается максимальный по модулю коэффициент при неизвестной в уравнениях с номерами Этим гарантируется, что для всех переменных и уравнений

В схеме главного выбора допускается нарушение естественного порядка исключения неизвестных. Здесь на первом шаге среди всех элементов определяется максимальный по модулю элемент Первое уравнение системы и уравнение с номером меняются местами. Затем производится исключение неизвестного Из всех уравнений, кроме первого. На всех других шагах последовательность действий аналогичная.

< Предыдущая		Следующая >