19. Квадратурные формулы Гаусса

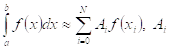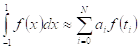Итак, все квадратурные формулы имеют вид - веса. Формулы Гаусса строятся также по общему виду с дополнительным условием: формула должна быть точной для многочленов наиболее высокой степени. Как правило, формулы Гаусса сначала строятся для отрезка , то есть , а затем с помощью замены осуществляется переход к формулам интегрирования на произвольном отрезке:

Требование точности формулы для многочленов степени эквивалентно требованию ее точности для функции (базис для ). Следовательно,

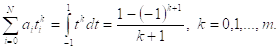(4.8.1)

Уравнение (4.8.1) дает систему нелинейных уравнений для определения Этих переменных штук. Следовательно, необходимый многочлен будет иметь степень , так как нужно учесть, что Построим, например, квадратурную формулу Гаусса с двумя и тремя узлами.

А). Индекс пробегает значения То есть - два узла. По формуле (4.8.1) получим

Итак, соответствующая нелинейная система уравнений имеет вид

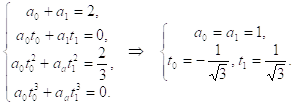
Таким образом, получаем квадратурную формулу Гаусса:

(4.8.2)

Точную для многочленов третьей степени.

Б). Формула (4.8.1) дает

Итак, квадратурная формула Гаусса в случае б) имеет вид

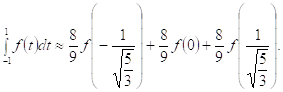(4.8.3)

Она точна до многочленов пятой степени.

Для квадратурной формулы Гаусса справедлива следующая оценка погрешности:

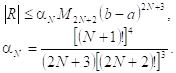(4.8.4)

Ее коэффициенты убывают очень быстро, например,

< Предыдущая		Следующая >