01. Функция одной переменной: способы задания, характеристики поведения. Примеры функциональных зависимостей

Точный математический анализ социально-экономических проблем всегда базируется на понятии функции. Функция - это правило, по которому элементы одного числового множества сопоставляются с элементами другого числового множества. Функции обозначаются как:

, где

х - аргумент функции, объясняющая или независимая переменная, у – значение функции, объясняемая или зависимая переменная.

Существуют четыре способа задания функции: табличный, графический, аналитический, алгоритмический. Некоторые из перечисленных способов задания функций (иногда говорят "функциональных зависимостей") будут рассмотрены ниже на конкретных примерах.

Пример 1: Результаты изучения сезонного спроса на некоторый товар приводятся в таблице.

№	Период времени	Спрос, тыс. шт.
1	1	3
2	2	5
3	3	12
4	4	9
5	5	6
6	6	2
7	7	3

Для каждого конкретного момента времени в таблице указывается значение спроса на товар в этот момент времени, то есть правило задано таблично.

Пример 2: Изучение спроса на некоторый товар в зависимости от изменения цены на него позволило построить следующую графическую зависимость:

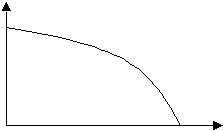
Графический способ представления, как очевидно является наиболее удобным с точки зрения очевидности представления данных, но наименее удобным с позиций точности.

Пример 3. Расход продуктов питания Y в зависимости от доходов семьи Х может быть описан следующей зависимостью

Пример 4. Издержки по управлению товарными запасами У Складываются из затрат на хранение и затрат на доставку. В свою очередь каждое слагаемое зависит от объема товарной массы

Где А, b - коэффициенты, характеризующие условия хранения и поставки товара.

Пример 5: В микроэкономике, изучающей поведение потребителя на рынке товаров и услуг, широко используется функция полезности U. Для случая двух товаров, например, чая и кофе, она может иметь вид:

Здесь У1,У2 - объемы потребления каждого вида товара.

Приведённых примеров достаточно, чтобы сделать некоторые выводы.

Во-первых, Аналитические зависимости (формулы) совершенно различны, но все они состоят из конечного числа простых зависимостей, которые называют основными элементарными функциями.

На рис.1 показаны шесть основных элементарных функций (по порядку слева направо):

1. Линейная -

2. Квадратичная

3. Гипербола

4. Логарифмическая

5. Показательная

6. Степенная

Используемые на практике функции состоят из сочетаний нескольких элементарных и строятся по принципу "функция от функции". Например, пусть z = F(y). В свою очередь, переменная У также является функцией, зависящей от х - то есть у = F(x). Тогда говорят, что функция z является сложной функцией вида Z = F(f(x)).

Можно отметить, что функция может зависеть от одной переменной, тогда её можно изобразить на плоскости в виде графика в системе координат. Если аргумента два, как у функции полезности, то она может быть изображена на плоскости в виде совокупности линий уровня (см. рис.2).

Во-вторых, каждый из перечисленных способов задания функции не исключает любой другой. Они лишь дополняют друг друга. В одних задачах удобнее использовать аналитическую зависимость, а в других - графическую.

Кроме этого, можно отметить, что можно производить переход от одного способа представления функций к другому.

В-Третьих, функциональные зависимости полезны не только тем, что позволяют вычислить объясняемую переменную при заданных значениях объясняющих переменных, но и тем, что позволяют выявить качественные особенности описываемого явления.

Например, исследуем как изменяются затраты на продукты питания (см. пример 2), если доход увеличивается на величину Dх. Новое значение затрат определится как

Таким образом очевидно, что увеличение затрат на питание не зависит от дохода Х, а зависит лишь от прироста дохода Dх. Это означает, что, если индивид получал 800 руб. в месяц и его зарплата увеличится на 20 руб., то из этой величины он выделит дополнительно на питание 14 руб. То же самое сделает другой человек при зарплате 1600 руб. в месяц, если его зарплата также увеличится на 20 руб.

Следующая >