3. Исчисление высказываний
Исчисление высказываний (теория L) определяется следующими компонентами.
1. Алфавит составляют:
· Пропозициональные буквы (от англ. proposition – высказывание) – заглавные буквы латинского алфавита (иногда с индексами – натуральными числами): 
,
, 
,
,
,…
· Логические связки: 
.
· Скобки: (, ).
Иногда в исчислении высказываний допускаются формулы с другими логическими связками, но при этом учитывается, как они выражаются через инверсию и импликацию. Так, 
, 
. Такие записи являются удобными сокращениями.
2. Формулы определяются так же, как в главе 1.
Определение. 1) Всякая пропозициональная буква есть формула.
2) Если 
, 
– формулы, то формулами являются также 
, 
.
3) Символ является формулой тогда и только тогда, когда это следует из 1) и 2).
3. Аксиомы задаются тремя схемами аксиом:
А1. 
.
А2. 
.
А3. 
.
Существуют исчисления высказываний с другим набором логических связок и другими схемами аксиом, но в данном пособии они не рассматриваются. Желающие могут ознакомиться с ними в [12].
4. Правило вывода Modus ponens (сокращенно MP) – правило отделения (лат.).
├.
Здесь , – любые формулы. Таким образом, множество аксиом исчисления высказываний, заданное тремя схемами аксиом, бесконечно. Множество правил вывода задано одной схемой, и также бесконечно.
Теорема. Все теоремы исчисления высказываний – тавтологии.
Доказательство. Докажем сначала, что аксиомы А1 – А3 являются тавтологиями.
Предположим, что
Полученное противоречие доказывает, что аксиома А1 – тавтология.
Предположим, что
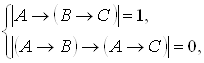
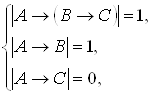
Полученное противоречие доказывает, что аксиома А2 – тавтология.
Предположим, что
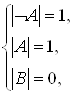
Полученное противоречие доказывает, что аксиома А3 – тавтология.
Таким образом, все аксиомы исчисления высказываний представляют собой тавтологии. Теоремы выводятся по правилу вывода MP, следовательно, по ранее полученным результатам (см. Глава 1. Высказывания, формулы, тавтологии.), также являются тавтологиями, что и требовалось доказать.
Следствие. Исчисление высказываний непротиворечиво.
Доказательство. Предположим противное, то есть в исчислении есть теоремы и . По доказанной теореме, и являются тавтологиями (тождественно истинными формулами), следовательно, формула одновременно является тождественно истинной и тождественно ложной, что является противоречием.
Лемма. ├
.
Доказательство. Построим вывод формулы .
1. 
. А1 с подстановкой вместо – .
2. 
. А1 с подстановкой вместо – .
3. 
А2 с подстановкой вместо 
– , а вместо –.
4. 
. МР 2,3.
5. . МР 1,4.
Что и требовалось доказать.
Теорема дедукции. Пусть 
– множество формул, , – формулы. Тогда , ├
├.
В частности, если 
, то если ├├.
Доказательство. Пусть , 
, …, 
, – вывод из и . Методом математической индукции докажем, что ├
, 
.
1) Проверим, что утверждение ├ справедливо при 
, то есть ├
.
Для возможны три варианта: 
, – аксиома, 
.
А) Пусть или – аксиома. Построим вывод:
1. .
2. 
. А1 с подстановкой вместо – , вместо – .
3. . МР 1, 2.
Таким образом, ├.
Б) Пусть . По лемме, ├
. Таким образом, ├.
2) Пусть утверждение ├ верно при 
, 
. Докажем утверждение для 
, то есть ├
.
Для формулы 
есть следующие возможности: 
, – аксиома, 
, которые рассматриваются аналогично предыдущему пункту, и новая возможность: получается из предыдущих формул , , …, 
, по правилу Modus ponens. Последний случай рассмотрим подробно.
Среди формул , , …, есть формулы (может быть, и не одна) вида 
, 
, такие, что имеет место формула 
(которая также присутствует в выводе), поэтому и возможно применение правила Modus ponens.
По предположению индукции, ├
, ├
.
Построим вывод:
1. .
2. .
3. 
. А2 с подстановкой вместо – , вместо – .
4. 
. МР 2, 3.
5. .
Таким образом, доказано, что ├, следовательно, по методу математической индукции, ├
, то есть ├. Теорема доказана.
Справедлива и обратная теорема.
Теорема. ├
, ├.
Доказательство. Построим вывод:
1. .
2. .
3. . По условию теоремы, эта формула выводима из .
4. . МР 2, 3.
Теорема доказана.
На основании теоремы дедукции получена теорема о полноте исчисления высказываний. Доказательство этой теоремы довольно громоздко, поэтому желающие могут ознакомиться с ним в [12].
Теорема о полноте. Всякая тавтология является теоремой исчисления высказываний.
Следствие. Множество всех теорем исчисления высказываний совпадает с множеством всех тавтологий.
Теорема дедукции позволяет строить выводы многих формул в исчислении высказываний.
| < Предыдущая | Следующая > |
|---|
