07. Булевы функции
P Логической, Или Булевой, переменной называется переменная, принимающая одно из двух значений 0 и 1, которые интерпретируются как «ложь» и «истина» соответственно.
P Булевой функцией 
называется функция N булевых переменных, принимающая одно из двух значений 0 и 1, которые интерпретируются как «ложь» и «истина» соответственно.
Булевы функции задаются таблицами истинности или логическими формулами.
Например, булева функция, заданная формулой 
, задаётся следующей таблицей истинности:
|
|
|
|
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
Переменная 
(I = 1, …, N) булевой функции 
называется Существенной, если найдутся такие наборы значений переменных 
и 
, при которых выполняется условие
.
В противном случае переменная называется Фиктивной.
Пример. Определить существенные переменные булевой функции 
.
Решение. Составим таблицу истинности данной функции:
|
Х1 |
Х2 |
Х3 |
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
Переменная Х3 является существенной для данной булевой функции, так как 
. Переменная 
является фиктивной, так как 
, 
, 
, 
. Переменная 
также является фиктивной, так как 
, 
, 
, 
.□
Теорема 1.6. Булеву функцию всегда можно задать формулой, не содержащей фиктивных переменных.
Например, Применим равносильности теоремы 1.1 (см. пункт 1.3) для преобразования булевой функции рассмотренного выше примера:
.
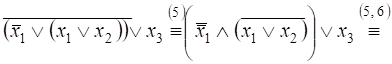
Задачи и упражнения
1.29. Приведите пример булевой функции четырёх переменных.
1.30. Постройте булеву функцию, отражающую работу устройства, состоящего из трёх узлов. Устройство пропускает сигнал, если его пропускает большинство узлов этого устройства.
1.31. Найдите существенные переменные булевой функции
.
1.32. Найдите фиктивные переменные булевой функции
.
1.33. Задайте булеву функцию в задаче 1.32 формулой, не содержащей фиктивных переменных.
| < Предыдущая | Следующая > |
|---|
