06. Применение языка логики предикатов для записи математических предложений

При формулировке определений математических понятий используются слова «называется», «обозначается», «говорят, что». Слово «если» в тексте определения имеет логическую интерпретацию «тогда и только тогда, когда».

Определения записываются в виде Эквиваленции.

Например, Определение предела функции , заданной на множестве формулируется следующим образом: действительное число A называется пределом функции в точке , если для любого сколь угодно малого положительного числа ε найдется положительное число δ, зависящее от ε, такое, что для всех X, удовлетворяющих условию , выполняется неравенство .

Символически это определение записывается так:

,

Где .

В формулировках математических Теорем выделяются три части: условие теоремы, заключение теоремы и разъяснительная часть. УСловие теоремы – это предикат , определённый на множестве . Заключение теоремы – это предикат , определённый на множестве . Разъяснительная часть – Это описание объектов теоремы.

Теоремы такой структуры формулируются в виде Импликации:

. (1.6.1)

Предикат называется Достаточным условием для предиката , а – Необходимым условием для .

Исходя из Прямой теоремы (1.6.1), формулируются новые утверждения – верные или неверные:

Обратная теорема ;

Противоположная теорема ;

Обратная противоположной теорема .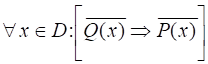

Например, для предикатов и, определённых на множестве D геометрических векторов числового пространства, формулируются теоремы:

1. Прямая теорема: если два вектора ортогональны, то их скалярное произведение равно нулю:

;

2. Обратная теорема: если скалярное произведение двух векторов равно нулю, то эти два вектора ортогональны:

;

3. Противоположная теорема: если два вектора не ортогональны, то их скалярное произведение отлично от нуля:

;

4. Обратная противоположной теорема: если скалярное произведение двух векторов отлично от нуля, то эти два вектора не ортогональны:

.

Теорема 1.5. 1) Прямая теорема и теорема, обратная противоположной, равносильны.

2) Обратная теорема и противоположная теорема равносильны.

Если верны и прямая, и обратная теоремы, то формулируются теоремы другой структуры. В этом случае каждый из предикатов и является Необходимым и достаточным условием для другого. Теоремы такой структуры формулируются в виде Эквиваленции: .

Например, для предикатов и , определённых на множестве D геометрических векторов числового пространства, формулируется теорема о необходимом и достаточном условии ортогональности двух векторов: два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.

.

Задачи и упражнения

1.24. Введите предикаты и с их помощью запишите следующие определения:

1) чётной функции;

2) непрерывности функции в точке.

1.25. Введите предикаты и с их помощью запишите следующие теоремы:

1) необходимое условие сходимости числового ряда;

2) достаточное условие интегрируемости функции на отрезке;

3) необходимое и достаточное условие совместности системы линейных уравнений.

1.26. Установите для каждого из следующих условий, является ли оно необходимым для того, чтобы выполнялось неравенство :

1) ;

2) ;

3) ;

4) .

1.27. Установите для каждого из следующих условий, является ли оно достаточным для того, чтобы выполнялось неравенство :

1) ;

2) ;

3) ;

4) .

1.28. Выберите среди следующих предложений те, которые после подстановки вместо многоточий слов «необходимо и достаточно» обращаются в верные утверждения.

1) Условие … для того чтобы .

2) Для того чтобы четырёхугольник являлся параллелограммом… чтобы он имел центр симметрии.

3) Для того чтобы выполнялось условие … чтобы выполнялось условие .

4) Условие … для того чтобы выполнялось условие .

< Предыдущая		Следующая >