04.3. Исчисление предикатов

Построение исчисления предикатов осуществляется, с одной стороны, аналогично построению исчисления высказываний, а с другой – качественно отличается от него.

Сходство и даже связь между обоими исчислениями заключается, во-первых, в том, что значение, которое принимает пропозициональная функция (предикат) из универсума рассуждения, при соответствующих аргументах может быть либо истинным, либо ложным. Во-вторых, все логические связки (операторы), которые рассматривались в предыдущей главе – отрицание, дизъюнкция, конъюнкция, импликация – используются и в исчислении предикатов. Следовательно, для определения истинностного значения пропозициональной функции таблица истинности, с которой мы знакомы, может применяться в принципе и здесь, однако на практике такой способ оказывается крайне громоздким и неэффективным.

Прежде всего в исчислении предикатов используются кванторы. Кроме того, для определения истинности пропозициональной функции необходимо установить определенное соответствие между функцией и теми независимыми переменными (аргументами), которые составляют область ее определения (универсум рассуждения). Например, если универсум для отношения Х < у составляет множество пар целых положительных чисел, то для определения значения истинности этого отношения необходимо установить соответствие (функцию) между любой парой чисел Х и У из универсума и отношением х < у. Очевидно, что при Х = 2 и У = 3 высказывание, полученное путем подстановки этих чисел в формулу, будет истинным, а при Х=5 И у=3– ложным.

Функция, которая соотносит независимым переменным из ее универсума соответствующее значение истинности или ложности, называют Логической, интерпретационной или Семантической.

В общем случае, если предикат Р зависит от П индивидных (предметных) переменных, т. е. Р (х1, х2,..., XN), то каждой П-ке переменных из универсума семантическая функция будут соотносить значение "истина" или "ложь". Если N=0, мы получим отдельное, нерасчлененное высказывание (законы исчисления таких высказываний рассматривались в предыдущей главе). Следовательно, исчисление высказываний может быть получено в качестве частного случая исчисления предикатов, а тем самым устанавливается связь между ними. При П = 1, т. е. Р(х), предикат является свойством, при П = 2, 3, 4 получаем бинарные, тернарные и тому подобные отношения.

Поскольку в исчислении предикатов применяются кванторы, при определении истинностного значения пропозициональной функции необходимо установить процедуру для вычисления формул вида:

(х) А и (Ех) А,

Где А, как обычно, обозначает любую формулу предметного языка.

Их значения мы сможем вычислить лишь тогда, когда сумеем соотнести некоторую семантическую функцию с в формуле А. Другими словами, когда при произвольном выборе элемента Х из универсума – причем свободно входящего в формулу А – сможем приписать А в качестве ее значения семантическую функцию с. Тогда будем считать, что формула (х) А будет истинна, если приписанная ей семантическая функция будет всегда принимать значение истины. В противном случае (х) А будет ложно. Аналогично этому (Ех) А будет истинно, если среди значений его семантической функции найдется по крайней мере одно истинное утверждение. В противном случае оно будет считаться ложным.

Опираясь на эти определения, мы можем теперь вычислить таблицу истинности для произвольной формулы, например, формулы, универсум которой состоит всего из двух объектов: 1 и 2.

Чтобы вычислить истинностные значения, например, формулы

Р(у) v (х) (Р(х) → Q).

Необходимо учесть определенное распределение, состоящее из семантической функции для Р(х), значения истинности подформулы Q и значения для свободной переменной У. В связи с этим на входах таблицы истинности для рассматриваемой формулы будут три величины. Но предварительно следует выписать список четырех (22) распределений значений истины семантической функции одной переменной для универсума |1, 2| (табл.12).

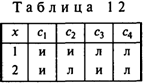
Основываясь на этом распределении, можно вычислить таблицу истинности для рассматриваемой функции (табл.13).

Таблица 13

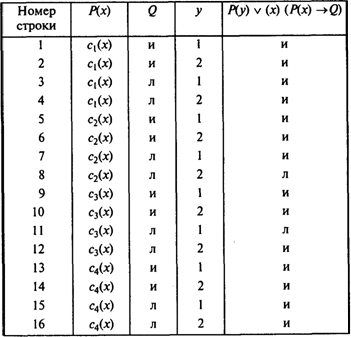
Этот пример показывает, что построение таблицы истинности для исчисления предикатов составляет несравненно более трудную задачу, чем построение таблицы для исчисления высказываний. В самом деле, если универсум рассуждения будет состоять из 10 элементов, то для этого придется построить 210 = 1024 семантические функции только для одной независимой переменной, а число строк в таблице в огромной степени возрастает по мере усложнения формул. В нашем примере речь шла только о двух объектах универсума рассуждений, а формула была крайне проста. Поэтому к таблицам истинности в исчислении предикатов обращаются главным образом для иллюстраций, используя для этого весьма простые формулы с крайне ограниченным универсумом рассуждений.

Тем не менее аналогия с исчислением высказываний оказывается весьма полезной для объяснения таких понятий, как Общезначимая (или Тождественно истинная) формула исчисления предикатов и Логическое следование в этом исчислении. Формула А считается общезначимой в исчислении предикатов, если при всяком выборе универсума рассуждений (области ее значений) столбец ее значений в таблице будет состоять только из истин. Если универсум будет фиксирован, то формула называется общезначимой только в этом универсуме.

Поскольку проверка формулы на общезначимость, как мы видели, представляет собой крайне трудную задачу, то выход часто ищут в противоположной операции: в установлении необщезначимости формулы. Для этого в принципе достаточно найти такую единственную строку в таблице, где формула принимает ложное значение. В приведенном выше примере (см. табл.13) этими строками являются 8 и 11.

В некоторых случаях поиск необщезначимой формулы может быть ускорен, если воспользоваться сокращенными способами, основанными на определениях логических операций дизъюнкции, конъюнкции и импликации. Например, если нам было бы известно, что один из дизъюнктивных членов рассматриваемой формулы был бы истинен, тогда истинной была бы вся формула. Если же ложным оказался один член конъюнкции, то вся формула окажется ложной.

< Предыдущая		Следующая >