25. Формирование списка кандидатов на ветвление
После вычисления каждой из оценок ![]() (I = 1,2) следует проверить, не состоит ли множество
(I = 1,2) следует проверить, не состоит ли множество ![]() из единственного маршрута. Если в каждой строке и в каждом столбце матрицы
из единственного маршрута. Если в каждой строке и в каждом столбце матрицы ![]() оказалось лишь по одному элементу, отличному от +¥, то множество
оказалось лишь по одному элементу, отличному от +¥, то множество ![]() содержит единственный маршрут, длина которого равна
содержит единственный маршрут, длина которого равна ![]() . В этом случае верхняя граница (наименьшее из уже вычисленных значений F(X)) полагается равной минимуму из предыдущего значения Z0 и
. В этом случае верхняя граница (наименьшее из уже вычисленных значений F(X)) полагается равной минимуму из предыдущего значения Z0 и ![]() , т. е.
, т. е.
Z0 = min {Z0, ![]() }.
}.
Если ![]() содержит более одного маршрута и
содержит более одного маршрута и ![]() меньше текущего значения Z0, то множество
меньше текущего значения Z0, то множество ![]() включается в число кандидатов на ветвление. Остановка производится, если наименьшая из оценок снизу кандидатов на ветвление не меньше текущего значения Z0.
включается в число кандидатов на ветвление. Остановка производится, если наименьшая из оценок снизу кандидатов на ветвление не меньше текущего значения Z0.
Пример 5.2. Решить методом ветвей и границ задачу коммивояжера с матрицей

Возьмем в качестве произвольного допустимого маршрута:
X0 = {(1,2), (2,3), (3,4), (4,5), (5,1)}.
Тогда F(X0) = 10 + 10 + 20 + 15 + 10 = 65 – текущее значение Z0 – (верхняя граница длин всех маршрутов).
Получим редуцированную матрицу ![]() .
.
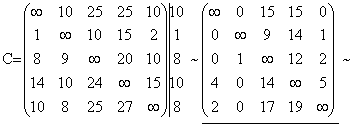
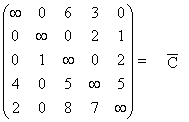
0 0 9 12 0
Нижняя граница D(X) = 10 + 1 + 8 + 10 + 8 + 9 + 12 = 58. Данное значение является нижней границей длин всех маршрутов. Заметим, что в идеальном случае поиск решения заключался бы в выборе ровно одного нулевого элемента в каждой строке и каждом столбце. Другими словами, если бы такой маршрут нулевой длины мог быть найден, то длина оптимального маршрута равнялась бы 58. Исходя из верхней и нижней границ, можно заключить, что 58 ≤ F(X*) ≤ 65.
Выберем дугу (r, s) с помощью вычисления значений функции Q(m, n).
Q(1,2) = 0, Q(2,1) = 0, Q(3,1) = 0, Q(4,2) = 4, Q(1,5) = 1, Q(2,3) = 5, Q(3,4) = 2, Q(5,2) = 2.
Следовательно, Q(r, s) = Q(2,3). Осуществим разбиение (ветвление). Правое подмножество X2 будет содержать все маршруты, которые исключают дугу (2,3). Поэтому C2 (2,3) = +∞.
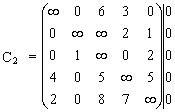
![]() ~
~
![]() ~
~  =
= ![]()
![]()
Оценка снизу для правого подмножества X2 определяется следующим образом:
D(X2) = D(X) + Θ(2,3) = 58 + 5 = 63 < Z0.
Левое подмножество X1 будет содержать маршруты, которые всегда включают дугу (2,3), и поэтому вторая строка и третий столбец в матрицу C1 не включаются. В результате будем иметь матрицу на единицу меньшего размера. Далее необходимо положить C1 (3,2) = +∞, чтобы запретить подцикл {(2,3),(3,2)}. В результате получим матрицу
![]()
C1 = 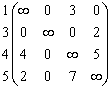 =
=![]() .
.
Оценка снизу для левого подмножества:
D(X1) = D(X) + t = 58 + 0 = 58 < Z0,
Где t – константа приведения матрицы С1
В списке кандидатов на ветвление множества X1 и X2. Так как D(X1) < D(X2), будем производить ветвление множества X1. Выберем дугу (r, s) с помощью значений функции Q(m, n) для матрицы.
Q(1,2) = 0, Q(1,5) = 2, Q(3,1) = 2, Q(3,4) = 3, Q(4,2) = 4, Q(5,2) = 2.
Следовательно, Q(r, s) = 4, (r, s) = (4,2).
Правая подматрица:
![]()
![]()
C4 =  ~
~  =
= ![]() .
.
![]()
Оценка снизу для правого подмножества:
D(X4) = D(X1) + Θ(4,2) = 58 + 4 = 62 < Z0.
Левая подматрица. Левое подмножество X3 будет содержать маршруты, которые всегда включают дугу (4,2), и поэтому четвертая строка и второй столбец в матрицу C3 не включаются. В результате будем иметь матрицу на единицу меньшего размера. Далее необходимо положить C3 (3,4) = +∞, чтобы запретить подцикл {(4,2),(2,3),(3,4)}. В результате получим матрицу
![]()
![]()
C3 = 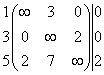 ~
~ 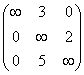 ~
~  =
= ![]() .
.
![]()
D(X3) = D(X1) + t = 58 + 5 = 63 < Z0.
В списке кандидатов на ветвление множества X3, X4, X2.
Минимальная нижняя оценка оказалась у множества X4, следовательно, для дальнейшего разбиения выбираем множество X4.
Определим дугу (r, s) с помощью значений функции Q(m, n) для матрицы ![]() .
.
Q(1,2) = 0, Q(1,5) = 1, Q(3,1) = 0, Q(3,4) = 3, Q(4,1) = 1, Q(5,2) = 2.
Следовательно, Q(r, s) = 3, (r, s) = (3,4).
Правая подматрица:
![]()
![]()
C6 =  ~
~  =
= ![]() .
.
Оценка снизу для правого подмножества:
D(X6) = D(X4) + Θ(3,4) = 62 + 3 = 65 = Z0.
Следовательно, множество X6 исключаем из списка.
Левая подматрица. Левое подмножество X5 будет содержать маршруты, которые всегда включают дугу (3,4), и поэтому третья строка и четвертый столбец в матрицу C5 не включаются. В результате будем иметь матрицу на единицу меньшего размера. Далее необходимо положить C5 (4,2) = +∞, чтобы запретить подцикл {(2,3), (3,4), (4,2)}, однако это условие оказалось уже выполненным. В результате получим матрицу
![]()
C5 =  =
= ![]() .
.
Оценка снизу для левого подмножества:
D(X5) = D(X4) + t = 62 + 0 = 62 < Z0.
В списке кандидатов на ветвление множества X3, X5, X2.
Минимальная нижняя оценка оказалась у множества X5, следовательно, для дальнейшего разбиения выбираем множество X5. Определим дугу (r, s) с помощью значений функции Q(m, n) для матрицы ![]() .
.
Q(1,2) = 0, Q(1,5) = 1, Q(4,1) = 3, Q(5,2) = 2.
Следовательно, Q(r, s) = 3, (r, s) = (4,1).
Правая подматрица:
![]()
![]()
C8 = 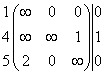 ~
~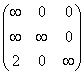 ~
~ 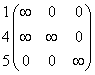 =
= ![]() .
.
![]()
Оценка снизу для правого подмножества:
D (X8) = D(X5) + Θ(4,1) = 62 + 3 = 65 = Z0.
Следовательно, множество X8 исключаем из списка.
Левая подматрица. Левое подмножество X7 будет содержать маршруты, которые всегда включают дугу (4,1), и поэтому четвертая строка и первый столбец в матрицу C7 не включаются. В результате будем иметь матрицу на единицу меньшего размера. Далее необходимо положить C7 (1,2) = +∞, чтобы запретить подцикл {(2,3), (3,4), (4,1), (1,2)}.
![]()
C7 = ![]() =
= ![]() .
.
Оценка снизу для левого подмножества:
D(X7) = D(X5) + t = 62 + 0 = 62 < Z0.
В списке кандидатов на ветвление множества X3, X7, X2. Множество X7 содержит единственный маршрут с минимальной нижней оценкой, поэтому задача решена.
X1 = ![]() = X*;
= X*;
Z0= F(X*) = 10 + 8 + 10 + 20 + 14 = 62.
Представим процесс решения в виде дерева (см. рис. 5.7).

Рис. 5.7.
Контрольные вопросы
1. Запишите задачу целочисленного линейного программирования.
2. Сформулируйте алгоритм метода ветвей и границ.
3. Перечислите область применения ЗЦЛП.
4. С какими трудностями приходится сталкиваться при алгоритмизации методов решения ЗЦЛП?
5. Приведите классификацию методов решения ЗЦЛП.
6. Какая задача называется задачей с ослабленными ограничениями?
7. Сформулируйте принцип ветвления в методе ветвей и границ.
8. Какую задачу решает понятие границы в методе ветвей и границ?
9. Сформулируйте постановку задачи коммивояжера.
10. Сформулируйте алгоритм метода ветвей и границ для решения задачи коммивояжера.
| < Предыдущая | Следующая > |
|---|