24. Ветвление

Процесс ветвления можно представить в виде дерева, каждая вершина которого соответствует некоторому множеству маршрутов, являющемуся подмножеством множества Х. При этом начальная вершина соответствует множеству всех маршрутов Х (рис. 5.6).

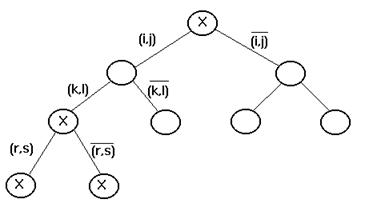
Рис. 5.6. Ветвление

На каждом шаге из числа кандидатов на ветвление выбирается множество Х1 с наименьшей оценкой. Оно разветвляется на два подмножества и . Подмножество состоит из всех маршрутов множества Х1, содержащих некоторую выбранную на данном шаге дугу (r, s), подмножество – из всех маршрутов множества Х1, не содержащих дуги (r, s).

Ребро дерева, соединяющее вершины Х1 и , помечается (r, s), а ребро дерева, соединяющее Х1 и , помечается .

Пусть – редуцированная матрица, соответствующая вершине Х1. Опишем способ выбора дуги (r, s). Он основан на стремлении сделать оценку поменьше, а оценку – больше, для того чтобы увеличить вероятность выбора для дальнейшего ветвления множества . Стремление к уменьшению приводит к выбору такой дуги (m, n), для которой

(m, n) = 0, (5.7)

Поскольку все маршруты множества содержат дугу (m, n). Стремление же увеличить приводит к выбору среди дуг, удовлетворяющих условию (5.7), той дуги, для которой значение функции

Максимально, т. е.

Смысл введения функции состоит в том, что величина является оценкой снизу для длины любого маршрута из Х1, не содержащего дуги (m, n), так как величина выражает дополнительное расстояние, которое коммивояжер проезжает в случае, когда в маршрут не включена дуга (m, n).

Построение редуцированных матриц И и вычисление оценок снизу

Положим:

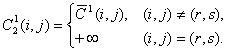
Искомая редуцированная матрица получается из с помощью описанной выше процедуры редуцирования. Сумма констант редуцирования равна при этом , а величина

= D(Х1) +

Является оценкой снизу для целевой функции F(X) на множестве .

Рассмотрим теперь множество . Все маршруты из этого множества содержат дугу (r, s). Найдем максимальный связанный путь, который принадлежит всем маршрутам множества Х1 и содержит дугу (r, s). Пусть этот путь начинается в городе m и заканчивается в городе t (может быть, m = r или t = s, или то и другое одновременно). Чтобы запретить подцикл, начинающийся и заканчивающийся в m, положим (T,M) = +∞. Остальные элементы матрицы полагаем равными соответствующим элементам матрицы , при этом строку, соответствующую городу r, и столбец, соответствующий городу s, в матрицу Не включаем, поскольку все маршруты из содержат дуги (r, s).

Редуцированная матрица расстояний для вершины получается из матрицы с помощью операции редуцирования. При этом оценка снизу для функции F(X) на множестве вычисляется по формуле

= D(Х1) + t,

Где t – сумма констант редуцирования.

< Предыдущая		Следующая >