14. Решение ЗЛП двухэтапным Симплекс-методом

Пример 3.14. Рассмотрим задачу

= 0,4X1+ 0,3X2 + 0,1X3 + 0,1X5 + 0,2X6 (3.71)

2X2 + 2X3 + 4X4 + X5 = 150

X1 + X2 + 2X5 = 200 (3.72)

X1 + X3 + 2X6 = 300

; j = 1,...,6 (3.73)

Так как ограничения (3.72) рассматриваемой ЗЛП уже имеют вид строгих равенств, то для приведения ее к каноническому виду достаточно только изменить знак функции На противоположный и рассмотреть задачу нахождения –0,4X1 – 0,3X2 –
– 0,1X3 – 0,1X5 – 0,2X6 (3.74) при тех же ограничениях (3.72)–(3.73).

Рассмотрим расширенную матрицу А системы уравнений (3.72)

Так как матрица А не содержит единичной подматрицы порядка 3, то она не является К-матрицей ЗЛП и, следовательно, к задаче (3.71)–(3.73) не может быть применен симплекс-метод.

Рассмотрим метод отыскания исходного опорного плана (К-матрицы)- метод искусcтвенного базиса.

ПЕРВЫЙ ЭТАП – РЕШЕНИЕ СПОМОГАТЕЛЬНОЙ ЗАДАЧИ

Пусть в ЗЛП (3.18) расширенная матрица системы линейных уравнений (3.63) не является К-матрицей. Рассмотрим следующую Вспомогательную задачу: найти вектор , максимизирующий функцию

(3.74)

При условиях

, (3.75)

, , , , . (3.76)

Переменные называются искусственными переменными вспомогательной задачи (ВЗ) (3.74–3.76). Обозначим множество планов ВЗ. Очевидно, что множество 0, так как вектор , а функция 0 ограничена сверху, следовательно, ВЗ (3.74–3.76) всегда разрешима, т. е. существует вектор такой, что = () = d.

Рассмотрим расширенную матрицу системы (3.75)

, (3.77)

Которая является К-матрицей ВЗ (3.74–3.76), т. е. ВЗ может быть решена симплекс-методом.

Предположим, что ВЗ решена симплекс-методом, на S-й итерации которого получен ее оптимальный опорный план

=, () = d, (3.78)

Определяемый К-матрицей ВЗ.

. (3.79)

Очевидно, что матрица

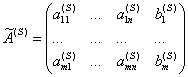(3.80)

Является расширенной матрицей системы линейных уравнений, равносильной системе (3.63).

Теорема 3.14. Если ( ) = d = 0 , то вектор =(,…, ) является опорным планом ЗЛП (3.18) , если ( ) = d < 0, то множество планов ЗЛП (3.18) пусто.

Из теоремы 3.14 следует, что при решении ВЗ (3.74–3.76) симплекс-методом могут представиться следующий три случая:

1. На S-й итерации симплексного метода ни одна из искусственных переменных не является базисной, (,), т. е. матрица =(3.61) является К-матрицей ЗЛП (3.18), а план =(, …, ) – опорным планом ЗЛП (3.18), определяемым этой К-матрицей.

2. На S-й итерации симплексного метода в числе базисных оказались искусственные переменные, например,

, p m,

Т. е.

= n + 1, = n + 1, …,= n + p,

Причем

.

Тогда вектор является вырожденным оптимальным опорным планом вспомогательной задачи линейного программирования, а матрица (3.61) содержит p < m единичных столбцов и не является К-матрицей основной задачи.

Однако в этом случае матрицу Можно преобразовать в К-матрицу основной задачи линейного программирования, определяющую ее исходный опорный план.

Для этой цели рассмотрим любую R-ю строку из первых Р строк матрицы ().

Среди элементов () этой строки есть хотя бы один элемент, отличный от нуля, так как в противном случае ранг матрицы А меньше m.

Выберем этот элемент в качестве направляющего и совершим один шаг метода Жордана–Гаусса преобразования матрицы с выбранным направляющим элементом. В результате базисная искусственная переменная будет заменена одной из основных переменных , а элементы (n + 1) столбца матрицы не изменятся.

После р таких шагов метода Жордана–Гаусса матрица будет преобразована в К-матрицу основной задачи линейного программирования, определяющую ее исходный опорный план

= (, …, ).

Очевидно, этот опорный план будет вырожденным.

3. На S-й итерации симплексного метода в числе базисных оказались искусственные переменные , p m, причем хотя бы одна не равна нулю. В этом случае множество Р планов ЗЛП (3.18) пусто.

ВТОРОЙ ЭТАП – РЕШЕНИЕ ИСХОДНОЙ ЗАДАЧИ

Если на первом этапе решение ВЗ закончилось случаем 1 или 2, то можно перейти ко второму этапу – решению исходной задачи.

(3.81)

(3.82)

, (3.83)

Так как расширенная матрица системы линейных уравнений (3.82) является К-матрицей.

< Предыдущая		Следующая >