05. Графический метод решения ЗЛП
Графическим методом целесообразно решать ЗЛП, содержащие не более двух переменных.
Алгоритм графического метода рассмотрим применительно к задаче:
![]() 3Х1 + 2Х2 (3.16)
3Х1 + 2Х2 (3.16)
При
Х1 + 2Х2 ![]() 6 (а)
6 (а)
2Х1 + Х2 ![]() 8 (б)
8 (б)
Р = Х1+0,8Х2 ![]() 5 (в) (3.17)
5 (в) (3.17)
-Х1 + Х2 ![]() 1 (г)
1 (г)
Х2 ![]() 2 (д)
2 (д)
Х1 ![]() 0, Х2
0, Х2 ![]() 0 (е)
0 (е)
Шаг 1. Строим область допустимых решений (3.17) – область Р, т. е. геометрическое место точек, в котором одновременно удовлетворяются все ограничения ЗЛП. Каждое из неравенств (а)–(д) системы ограничений (3.17) задачи геометрически определяет полуплоскость соответственно с граничными прямыми:
Х1 + 2Х2 = 6 (а)
2Х1 + Х2= 8 (б)
Х1+0,8Х2= 5 (в)
-Х1 + Х2= 1 (г)
Х2= 2 (д)
Условия неотрицательности переменных (е) ограничивают область допустимых решений первым квадратом. Области, в которых выполняются соответствующие ограничения (3.17) в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных (рис. 3.1).

Рис. 3.1
Если система неравенств (3.17) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям.
Полученная таким образом область допустимых решений Р – планов ЗЛП (см. рис. 3.1) есть многоугольник ABCDEF – замкнутое, ограниченное, выпуклое множество с шестью крайними, или угловыми, точками: A, B, C, D, E, F.
Шаг 2. Строим вектор-градиент ![]() линейной формы
линейной формы ![]()
![]() , указывающий направления возрастания функции
, указывающий направления возрастания функции ![]() .
.
Шаг 3. Строим прямую С1Х1 + С2Х2 = const – линию уровня функции ![]() , перпендикулярную вектору-градиенту
, перпендикулярную вектору-градиенту ![]() :
:
3Х1 + 2Х2 = const (рис.3.2).
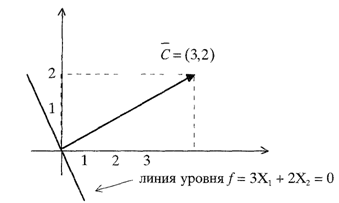
Рис. 3.2
Шаг 4. В случае максимизации ![]() передвигают прямую 3Х1 + 2Х2 = const в направлении вектора
передвигают прямую 3Х1 + 2Х2 = const в направлении вектора ![]() до тех пор, пока она не покинет область Р. Крайняя точка (или точки) области, в которой линия уровня покидает допустимую область, и является решением задачи (рис. 3.3).
до тех пор, пока она не покинет область Р. Крайняя точка (или точки) области, в которой линия уровня покидает допустимую область, и является решением задачи (рис. 3.3).
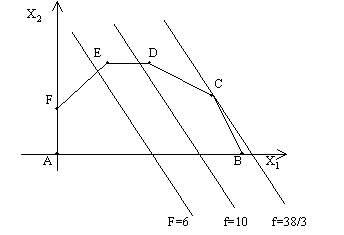
Рис. 3.3
Крайняя точка С – точка максимума ![]() , С =
, С = ![]() Лежит на пересечении прямых (а) и (б). Для определения ее координат решим систему уравнений:
Лежит на пересечении прямых (а) и (б). Для определения ее координат решим систему уравнений:
Х1 + 2Х2 = 6
2Х1 + Х2 = 8.
Откуда Х*1 = 10/3; X*2 = 4/3 или ![]() = (10/3; 4/3).
= (10/3; 4/3).
Подставляя значения Х*1 и X*2 в функцию ![]() , найдем
, найдем
max![]() =
= ![]() = 3 . 10/3 + 2 . 4/3 = 38/3.
= 3 . 10/3 + 2 . 4/3 = 38/3.
Замечания.
1. В случае минимизации ![]() Прямую С1Х1 + С2Х2 = const надо перемещать в направлении (-
Прямую С1Х1 + С2Х2 = const надо перемещать в направлении (-![]() ), противоположном
), противоположном ![]() .
.
2. Если допустимая область решений Р представляет собой неограниченную область и прямая при движении в направлении вектора ![]() (или противоположном ему) не покидает Р, то в этом случае
(или противоположном ему) не покидает Р, то в этом случае ![]() Не ограничена сверху (или снизу), т. е.
Не ограничена сверху (или снизу), т. е. ![]() (или
(или ![]() ).
).
Пример 3.1. Графическим способом решить ЗЛП
Max (2Х1 + Х2)
при
Х1 - Х2 ![]() 2 (1)
2 (1)
Х1 + 3Х2 ![]() 3 (2)
3 (2)
7Х1 - Х2 ![]() 2 (3)
2 (3)
Х1,2 ![]() 0.
0.
Шаг 1. Строим область Р (рис. 3.4). Она является неограниченной.
Шаг 2. Строим вектор ![]() .
.
Шаг 3. Строим линию уровня функции ![]() = 2Х1 + Х2 = const.
= 2Х1 + Х2 = const.
Шаг 4. Передвигая линию уровня в направлении вектора ![]() , убеждаемся в неограниченном возрастании функции
, убеждаемся в неограниченном возрастании функции ![]() , то есть
, то есть ![]() .
.
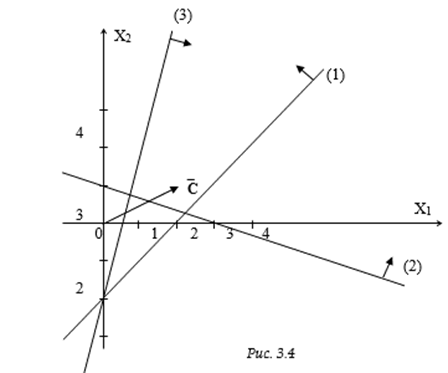
Пример 3.2. Решить графическим методом ЗЛП. Найти
![]() Х1 + 3Х2
Х1 + 3Х2
При ограничениях
2Х1 + 3Х2 ![]() 6 (1)
6 (1)
Х1 + 2Х2 ![]() 5 (2)
5 (2)
Х1 ![]() 4 (3)
4 (3)
0 ![]() Х2
Х2 ![]() 3 (4)
3 (4)

Рис. 3.5
Из рис. 3.5 видно, что область допустимых решений пуста (Р=![]() ).
).
Задача не имеет решения.
| < Предыдущая | Следующая > |
|---|