09. Пример решения заданий к разделу №3
Задание 1.
А) Найти предел функции 
Решение: Имеем неопределенность вида ![]() . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель
. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель ![]() , который при
, который при ![]() не равен нулю. В результате неопределенность будет раскрыта.
не равен нулю. В результате неопределенность будет раскрыта.
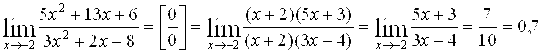
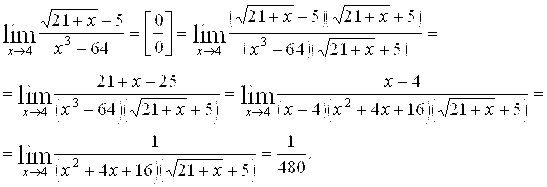
Найти предел функции 
Решение: Имеем неопределенность вида ![]() . Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение, стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель
. Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение, стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель ![]() , который при
, который при ![]() не равен нулю. В результате неопределенность будет раскрыта.
не равен нулю. В результате неопределенность будет раскрыта.
Найти предел функции 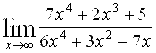
Решение: Имеем неопределенность вида ![]() . Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной X и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
. Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной X и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
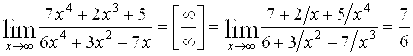 .
.
Или
 .
.
Найти предел функции 
Решение: Имеем неопределенность вида ![]() . Раскрываем ее аналогично тому как это сделано в примере 2.
. Раскрываем ее аналогично тому как это сделано в примере 2.

Б) Найти предел функции 
Решение: Имеем неопределенность вида ![]() . Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом
. Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом  .
.

Найти предел функции 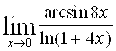
Решение: Имеем неопределенность вида ![]() . Для ее раскрытия воспользуемся теоремой о замене бесконечно малых функций эквивалентными им бесконечно малыми. Так как
. Для ее раскрытия воспользуемся теоремой о замене бесконечно малых функций эквивалентными им бесконечно малыми. Так как ![]() и
и ![]() , то
, то

Задание 2. Исследовать данную функцию на непрерывность и построить ее график

Решение:
Функция ![]() является неэлементарной, так как на разных интервалах представлена различными аналитическими выражениями. Эта функция определена на интервалах
является неэлементарной, так как на разных интервалах представлена различными аналитическими выражениями. Эта функция определена на интервалах ![]() , где она задана непрерывными элементарными функциями. Внутри каждого интервала указанные элементарные функции не имеют точек разрыва, следовательно, разрыв возможен только в точках перехода от одного аналитического выражения к другому, т. е. в точках
, где она задана непрерывными элементарными функциями. Внутри каждого интервала указанные элементарные функции не имеют точек разрыва, следовательно, разрыв возможен только в точках перехода от одного аналитического выражения к другому, т. е. в точках ![]() и
и ![]() .
.
Для точки ![]() имеем:
имеем:
![]() ,
, ![]() ,
, ![]() .
.
Так как ![]() , то функция
, то функция ![]() в точке
в точке ![]() имеет разрыв первого рода.
имеет разрыв первого рода.
Для точки ![]() находим:
находим:
![]() ,
,
![]() ,
,
![]() .
.
Так как ![]() , то функция
, то функция ![]() в точке
в точке ![]() имеет разрыв первого рода.
имеет разрыв первого рода.
График данной функции изображен на рис. 3.

Рис. 3.
Задание 3. Найти производную функции
А)![]()
Решение:

Б) 
Решение:

С) ![]()
Решение:
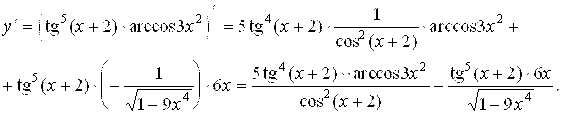
Задание 4. Найти максимальную прибыль, которую может получить фирма - производитель, при условии, что весь товар реализуется по фиксированной цене p=10 за единицу и известен вид функций издержек
С(x)= 20 +![]()
Решение:
Пусть х - количество реализованного товара, p - цена товара, C(x)- функция издержек, тогда прибыль от реализации произведенного товара равна
П(х)= p*x-C(x)
Найдем функцию прибыли.
П(х)=![]()
![]() Приравнивая производную функции прибыли к нулю, получаем уравнение
Приравнивая производную функции прибыли к нулю, получаем уравнение
![]() =0
=0
Корень уравнения х=5.
Проверка показывает, что максимальная прибыль достигается при х=5: Пmax(5)=5
Задание 5. Провести полное исследование функции и построить ее график

Решение:
Проведем полное исследование функции, используя следующую схему:
1. найти область определения функции;
2. исследовать на четность и нечетность функцию;
3. найти точки разрыва функции;
4. найти асимптоты (вертикальные, наклонные и горизонтальные) графика функции;
5. найти точки пересечения графика функции с координатными осями;
6. исследовать функцию на монотонность (указав интервалы возрастания и убывания) и экстремум;
7. определить интервалы выпуклости и вогнутости графика функции, точки перегиба;
8. при необходимости вычислить значения функции в дополнительных точках;
9. построить схематично график функции, используя результаты полученные в пунктах 1-8.
1. Областью определения функции является множество ![]() .
.
2. Так как 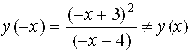 и
и ![]() , то функция не является ни четной, ни нечетной.
, то функция не является ни четной, ни нечетной.
3. Функция претерпевает разрыв в точке ![]() .
.
4. Найдем асимптоты графиков функции:
А). Прямая ![]() является вертикальной асимптотой, т. к.
является вертикальной асимптотой, т. к.
 ,
, 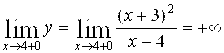
Б). Находим наклонные и горизонтальные асимптоты (горизонтальные асимптоты являются частным случаем наклонных асимптот) ![]() ,
,
Где 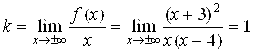 ;
;

Таким образом, прямая ![]() является единственной наклонной асимптотой и на
является единственной наклонной асимптотой и на ![]() , и на
, и на ![]() .
.
5. Найдем точки пересечения графика функции с осями координат.
А) С осью ![]() :
: ![]() ,
, ![]() , т. е. точка пересечения с осью
, т. е. точка пересечения с осью ![]() -
-  .
.
Б) С осью ![]() :
: ![]() ,
, 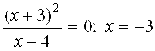 , т. е. точка пересечения с осью
, т. е. точка пересечения с осью ![]() -
- ![]() .
.
6. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.

Из ![]() получаем
получаем ![]() , откуда
, откуда ![]() ,
, ![]() .
.
+ _ +
![]() X
X
-3 11
Так как на интервалах ![]() и
и ![]() производная положительна, т. е.
производная положительна, т. е. ![]() , то график функции на указанных интервалах возрастает. Так как на интервале
, то график функции на указанных интервалах возрастает. Так как на интервале ![]() производная отрицательна, т. е.
производная отрицательна, т. е. ![]() , то на указанном интервале график функции убывает.
, то на указанном интервале график функции убывает.
Так как при переходе через точки ![]() ,
, ![]() производная функции меняет знаки и эти точки входят в область определения функции, то
производная функции меняет знаки и эти точки входят в область определения функции, то ![]() ,
, ![]() - точки локального экстремума. Причем
- точки локального экстремума. Причем ![]() точка локального минимума:
точка локального минимума: ![]() (так как при переходе через нее производная меняет знак с "+" на "-");
(так как при переходе через нее производная меняет знак с "+" на "-"); ![]() - точка локального максимума:
- точка локального максимума: ![]() (так как при переходе через нее производная меняет знак с "-" на "+").
(так как при переходе через нее производная меняет знак с "-" на "+").
7. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем вторую производную функции.

Очевидно, что в интервале ![]() вторая производная меньше нуля, т. е.
вторая производная меньше нуля, т. е. ![]() , и в этом интервале график функции является выпуклым вверх. В интервале
, и в этом интервале график функции является выпуклым вверх. В интервале ![]() вторая производная больше нуля, т. е.
вторая производная больше нуля, т. е. ![]() , и в этом интервале график функции является выпуклым вниз (вогнутым).
, и в этом интервале график функции является выпуклым вниз (вогнутым).
Несмотря на то, что при переходе через точку ![]() вторая производная меняет знак, она не является точкой перегиба, так как
вторая производная меняет знак, она не является точкой перегиба, так как ![]() не входит в область определения функции, т. е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.
не входит в область определения функции, т. е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.
Из ![]() получаем
получаем ![]() , откуда
, откуда ![]() ,
, ![]() .
.
+ _ +
![]() X
X
-3 11
Так как на интервалах ![]() и
и ![]() производная положительна, т. е.
производная положительна, т. е. ![]() , то график функции на указанных интервалах возрастает. Так как на интервале
, то график функции на указанных интервалах возрастает. Так как на интервале ![]() производная отрицательна, т. е.
производная отрицательна, т. е. ![]() , то на указанном интервале график функции убывает.
, то на указанном интервале график функции убывает.
Так как при переходе через точки ![]() ,
, ![]() производная функции меняет знаки и эти точки входят в область определения функции, то
производная функции меняет знаки и эти точки входят в область определения функции, то ![]() ,
, ![]() - точки локального экстремума. Причем
- точки локального экстремума. Причем ![]() точка локального минимума:
точка локального минимума: ![]() (так как при переходе через нее производная меняет знак с "+" на "-");
(так как при переходе через нее производная меняет знак с "+" на "-"); ![]() - точка локального максимума:
- точка локального максимума: ![]() (так как при переходе через нее производная меняет знак с "-" на "+").
(так как при переходе через нее производная меняет знак с "-" на "+").
8. График функции изображен на рис. 4.
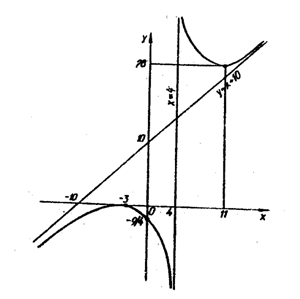
Рис. 4
| < Предыдущая | Следующая > |
|---|