03. Пример решения Заданий из раздела №1

Задание 1. Для данного определителя найти миноры и алгебраические дополнения элементов . Вычислить определитель : а) разложив его по элементам I-ой строки; б) разложив его по элементам J-го столбца; в) получив предварительно нули в I-ой строки.

I = 1, J = 2

Решение: 1. Находим миноры к элементам :

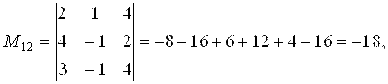
Алгебраические дополнения элементов соответственно равны:

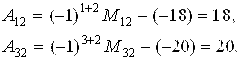
2. а). Вычислим определитель, разложив его по элементам первой строки:

Б) Вычислим определитель, разложив его по элементам второго столбца:

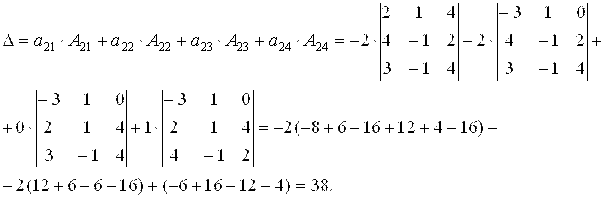
В) Вычисли определитель , Получив предварительно нули в первой строке. Используем свойство определителей: определитель Не ИЗмеНиТся, ЕСлИ ко всЕМ эЛеМентам кАКой-либо строки (столбца) прибавить СоотВЕтстВУющие эЛеМЕНтЫ другой строки (столбца), умноженНЫе на одно И то же произвольное число. Умножим третий столбец определителя на 3 и прибавим к первому, затем умножим на (-2) и прибавим ко второму. Тогда в первой строке все элементы, кроме одного, будут нулями. Разложим полученный таким образом опредЕЛитель по элемЕНтам первой строки и вычислим его:

В опрЕДЕЛитЕЛе трЕТьЕГо порядка получили нули в ПеРвом столбце по свойству тому же свойству определителей.

Задание 2.

Даны две матрицы A и B. Найти: а) AB; б) BA; в) ; г) .

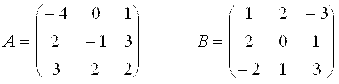
Решение: а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле . ИмеЕМ:

Б) Вычислим

ОчЕВидНО, что ;

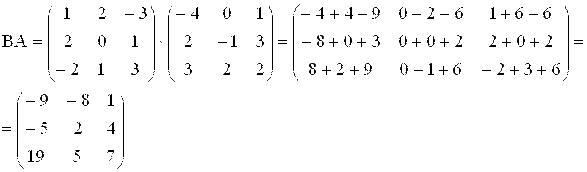
В) Обратная матрица матрицы А имеет виД

Где - алгебраическое дополнение, -минор, т. е. определитель полученный из основного определителя вычёркивание i-строки, j-столбца.

Т. е. матрица A - Невырожденная, и, значит, существуЕТ матрица . Находим:

Тогда

;

Г) Проверка

;

Задание 3. Проверить совместность линейной системы уравнений и в случае совместности решить ее а) по формулам Крамера б) методом Гаусса.

Решение: Совместность данной системы проверим по теореме Кронекера - Капелли. С помощью элементарных преобразований найдем ранг матрицы

Данной системы и ранг расширенной матрицы

Для этого умножим первую строку матрицы В на (-2) и сложим со второй, затем умножим первую строку на (-3) и сложим с третьей, поменяем местами второй и третий столбцы. Получим

Следовательно, (т. е. числу неизвестных). Значит, исходная система совместна и имеет единственное решение.

А) По формулам Крамера

Где -главный определитель, который мы посчитаем, например, по правилу треугольника

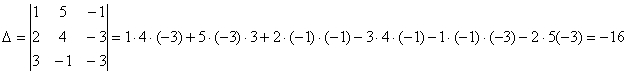Аналогично найдем

Находим: .

Б) Решим систему методом Гаусса. Исключим из второго и третьего уравнений. Для этого первое уравнение умножим на 2 и вычтем из второго, затем первое уравнение умножим на 3 и вычтем из третьего:

Из полученной системы находим .

Задание 4

Решить матричное уравнение

Пусть ,

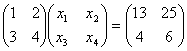решение матричного уравнения находим по формуле

Х=А -1В, где А -1 обратная матрица

- алгебраическое дополнение, где

- определитель, полученный из основного вычеркивание i-строки, j-столбца, - определитель матрицы.

Найдем обратную матрицу.

(-1)1+14=4

А12=(-1)1+23=-3

А21= (-1)2+12=-2

А22=(-1)2+21=1

DetA==1*4-2*3=4-6=-2

Итак,

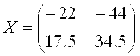
Задание 5

Предприятие выпускает три вида продукции, используя сырье трёх видов: . Необходимые характеристики указаны в таблице .

Вид сырья

Нормы расхода сырья на изготовление одного вида продукции, усл. ед.

Расход сырья за один день, усл. ед.

Сапог

Кроссовок

Ботинок

2700

900

1600

Найти ежедневный объем выпуска каждого вида продукции.

Решение: Пусть ежедневно фабрика выпускает x1 – единиц продукции первого вида, x2 - единиц продукции второго вида, x3 - единиц продукции третьего вида. Тогда в соответствии с расходом сырья каждого вида имеем систему.

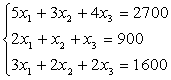
Решаем систему линейных уравнений любым способом. Решим данную систему, например, методом Гаусса. Составим матрицу из коэффициентов стоящих перед неизвестными и из свободных членов.

Обнуляем первый столбец, кроме первого элемента

1. Первую строчку оставляем без изменения

2. Вместо второй записываем сумму первой, умноженной на -2 и второй, умноженной на 5

3. Вместо третьей записываем сумму первой, умноженной на -3 и третьей, умноженной на 5

Аналогично обнуляем второй столбец под элементом второй строки второго столбца

˜˜

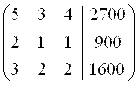Вернемся к системе

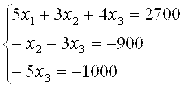
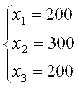
Т. е. фабрика выпускает 200- единиц продукции первого вида, 300- единиц продукции второго вида и 200- единиц продукции третьего вида.

Задание 6. Решить однородную систему линейных алгебраических

Уравнений.

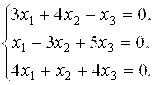
Решение: Так как определитель системы

То система ИМЕЕт бЕСчисленное множество решений. Поскольку , , возьмем любые два уравнения системы (наПРИМЕР, ПЕрвое И второе) и найдем ее рЕШение. ИмЕеМ:

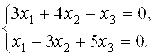
Так как определитель из коэффициентов при неизвестных и не равен нулю, то в качестве базисных нЕИзвестных ВОзьмЕМ и (хотя можно брать и другие пары нЕИзвЕСтных) И ПеРЕМЕСтим члЕНы с в правые частИ УравнЕНИЙ:

РЕШаЕМ пОСлЕдНюю систЕМу по формулам КрамЕРа :

Где

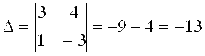Отсюда находим, что Полагая , где K—Произвольный коэффициент пропорциональности (произвольная постоянная), получаем решение исходной сИСтЕМы: .

< Предыдущая		Следующая >