4.2.10. Примеры решения задач по теме «Уравнение плоскости в пространстве»

Задача 1.

Составить уравнение плоскости, проходящей через точки А={5; -1; 3},

B={2; 2; 0}, C={-1; 1; 1}.

Указание

Для того, чтобы составить уравнение плоскости, нужно знать координаты

Точки, лежащей в этой плоскости, и координаты нормали, то есть вектора, перпендикулярного плоскости.

Решение

Рис. 6

Векторы АВ = (-3; 3; -3) и АС = (-6; 2; -2) параллельны данной плоскости, поэтому их векторное произведение или любой вектор, коллинеарный ему, является нормалью к плоскости.

Выберем в качестве нормали П = (0; 1; 1), а точкой {Х0; У0; Z0} будем считать точку В. Тогда уравнение плоскости имеет вид:

0·(Х – 2) + 1·(Y – 2) + 1·(Z – 0) = 0, Y + Z – 2 = 0.

Ответ: Y + Z – 2 = 0.

Задача 2.

Составить канонические уравнения прямой

Указание

Для того, чтобы составить канонические или параметрические уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты направляющего вектора, то есть вектора, коллинеарного прямой.

Решение

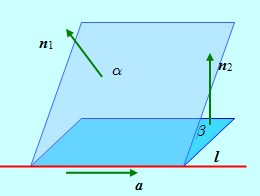
Рис. 7

Прямая является линией пересечения двух плоскостей, поэтому ее направляющий вектор А параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям П1 и П2 к данным плоскостям. В таком случае он коллинеарен векторному произведению [N1, N2].

N1 = (2; 1; -5), N2 = (5; 3; 8), [N1,N2] = (23; -41; 1).

Итак, (L; M; N) = (23; -41; 1).

Будем искать точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить единственным образом из системы уравнений, задающей пересекающиеся плоскости. Выберем для удобства вычислений Z0 = 0, тогда для точки М={Х0; У0; 0}

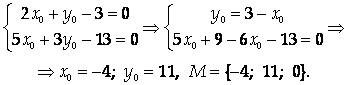
Теперь составим канонические уравнения данной прямой:

Ответ:

Задача 3.

Составить уравнение плоскости, проходящей через прямую L:

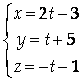
И точку М={2; -3; 1}.

Указание

Точка А={-3,5,-1} принадлежит плоскости, соответственно вектор параллелен плоскости. Кроме того, поскольку данная прямая лежит в плоскости, ее направляющий вектор A = (2: 1: -1) параллелен плоскости. Следовательно, нормаль к плоскости коллинеарна векторному произведению этих векторов.

Решение

Поскольку прямая лежит в плоскости, ее направляющий вектор A = (2: 1: -1) параллелен плоскости. При T = 0 из уравнений прямой получаем:

Координаты точки А, принадлежащей прямой и соОтВетственно плоскости.

Рис. 8

Тогда вектор АМ = (5; -8; 2) параллелен Плоскости. Следовательно, нормаль

П к плоскости коллинеарна векторному произведению [A, AM] = (-6; -9; - 21).

Выберем N = (2; 3; 7) и составим уравнение плоскости, проходящей через

Точку М перпендикулярно П:

2(Х – 2) + 3(У + 3) + 7(Z – 1) = 0, 2X + 3Y + 7Z – 2 = 0.

Ответ: 2X + 3Y + 7Z – 2 = 0.

Задача 4.

Найти кратчайшее расстояние между прямыми

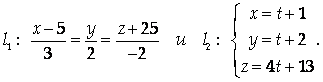
Указание

Координаты направляющих векторов данных прямых A1 = {3; 2; -2} и

A2 = {1; 1; 4} не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.

Составьте уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости; если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A.

Решение

Координаты направляющих векторов данных прямых A1 = {3; 2; -2} и

A2 = {1; 1; 4} не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.

Составим уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости (рис.9); если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A (рис.10).

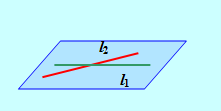
Рис. 9

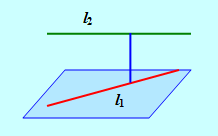
Рис. 10

[A1, A2] = (10; -14; 1) = N, точка А={5; 0; -25} лежит на прямой L1, следова-тельно, она лежит и в плоскости A. Тогда уравнение плоскости A имеет вид:

10(Х – 5) – 14(У – 0) + 1·(Z + 25) = 0; 10Х – 14У + Z – 25 = 0.

Точка В={1; 2; 13} принадлежит прямой L2. Проверим, лежит ли эта точка в плоскости A:

Тогда искомой величиной будет расстояние от В до A. Его можно найти, составив нормальное уравнение плоскости A:

Ответ: .

Задача 5.

Найти точку, симметричную точке А(5; -10; 4) относительно плоскости

A: Х – 3У + Z – 6 = 0.

Указание

Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ.

Решение

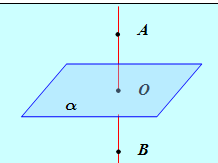
Рис. 11

Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ. Составим уравнения прямой АВ. Эта прямая перпендикулярна A, поэтому ее направляющим вектором можно считать нормаль к плоскости A: A = N = (1; -3; 1).

Параметрические уравнения прямой АВ имеют вид:

Точка О принадлежит и прямой АВ, и плоскости A, поэтому ее координаты должны удовлетворять и уравнениям прямой, и уравнению плоскости. Подставим в уравнение плоскости A параметрические выражения для X, Y, Z из уравнений прямой АВ:

T + 5 – 3(-3T – 10) + T + 4 – 6 = 0; 11T + 33 = 0; T = -3.

Итак, координаты точки О:

Поскольку точка О – середина отрезка АВ, то

Ответ: (-1; 8; -2).

< Предыдущая		Следующая >