4.1.4. Взаимное расположение прямых на плоскости

Пусть заданы уравнения двух прямых

Векторы П1 = (А1, В1) и П2 = (А2, В2) являются нормальными векторами для прямых L1 и L2 соответственно.

1. Условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности нормальных векторов П1 и П2, что эквивалентно пропорциональности координат этих векторов. Таким образом,

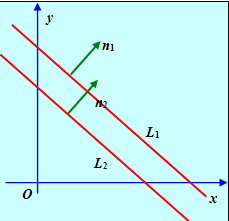
Рис. 6

2. Условие перпендикулярности прямых L1 и L2 эквивалентно условию ортогональности нормальных векторов П1 и П2, что эквивалентно равенству нулю скалярного произведения этих векторов. Таким образом,

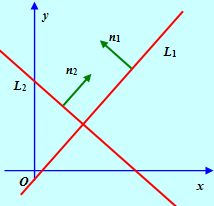
Рис. 7

3. Нахождение угла J между прямыми L1 и L2 сводится к нахождению угла между нормальными векторами П1 и П2. Имеем

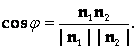
Тем самым

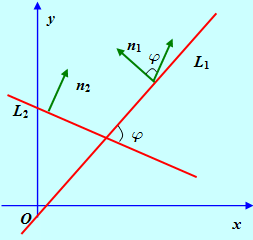
Рис. 8

Пример 2. Найдем угол между прямыми

Имеем

Следовательно,

Таким образом, угол между прямыми равен 30о.

Упражнение 1. При каких значениях параметра А прямые

А) параллельны, B) перпендикулярны?

Решение.

Нормальные векторы прямых П1 = (А + 1, 2), П2 = (1,-2А).

А) условие параллельности:

Решений нет, следовательно, прямые не могут быть параллельными ни при каком значении А.

B) условие пепрпендикулярности:

Ответ: параллельность невозможна; прямые перпендикулярны при А =

< Предыдущая		Следующая >