23. Некоторые предельные теоремы. Центральная предельная теорема

Центральная предельная теорема сыграла особую роль в развитии теории вероятностей, она имеет большое значение и для современных приложений. Центральная предельная теорема определяет условия, при которых суммы независимых случайных величин распределены асимптотически нормально.

Tеорема 1. Пусть X1,X2,…,Xn – взаимно независимые случайные величины с одной и той же функцией распределения F(X). Допустим, что М(Xk)=0, D(Xk)=1, K = 1, 2,..., N. При распределение нормированных сумм стремится к стандартному нормальному распределению.

Для доказательства используем метод характеристических функций. Характеристической функцией распределения F(X) (или случайной величины X) называется математическое ожидание случайной величины

Замечание. Мы вводили случайные величины как действительные функции, заданные на пространстве W. В данном случае под случайной величиной будем понимать пару действительных функций

Если X имеет плотность F(X), то

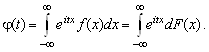
Например, характеристическая функция стандартного нормального распределения

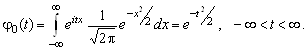
Если X – дискретная случайная величина,

где Xi – значение случайной величины X.

Замечание. Характеристическая функция распределения F(X) – это ни что иное как преобразование Лебега-Фурье функции F(X). Если X – непрерывная случайная величина, то характеристическая функция – это просто преобразование Фурье плотности распределения.

Докажем сначала, что характеристические функции распределения сумм Sn при и всех T cходятся к характеристической функции стандартного нормального распределения. Характеристическая функция суммы Sn

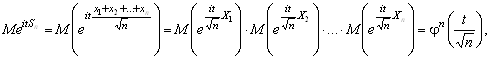
Где – характеристическая функция случайных величин Xk,

Поскольку математическое ожидание произведения независимых случайных величин равняется произведению их математических ожиданий, и все случайные величины X1,X2,…,Xn имеют одно и то же распределение, а значит и одну и ту же характеристическую функцию .

По формуле Тейлора

Полагая , получим

При больших N

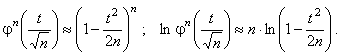
Поскольку То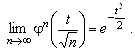

Докажем, что из сходимости характеристических функций следует сходимость функций распределения.

Из курса математического анализа известна теорема непрерывности: если F1(X), F2(X),..., Fn(X) - последовательность функций, ограниченных на всей числовой прямой, а - последовательность соответствующих преобразований Лебега-Фурье, сходящаяся к функции , то также является преобразованием Лебега-Фурье некоторой функции F0(X), а F0(X) является пределом функциональной последовательности F1(X), F2(X),..., Fn(X),... . Теорема непрерывности завершает доказательство Центральной предельной теоремы. §

Центральная предельна теорема позволяет понять природу случайных величин, имеющих нормальное распределение.

Пример 1. Рассмотрим распространение популяции деревьев. Если бы новые растения возникали только из семян, упавших с материнского дерева, то сеянцы были бы расположены около него. Тогда расстояние дерева N-ого поколения от исходного было бы распределено приблизительно нормально. При этих условиях площадь, покрытая потомками некоторого дерева, была бы пропорциональна его возрасту. ¨

Замечание 1. Если в условии Теоремы 1 М(Xk) = M, D(Xk) = s2, то распределение сумм

При cтремится к стандартному нормальному распределению. Действительно, если мы вместо случайных величин Xk рассмотрим , то попадем в условия Теоремы 1.

Замечание 2. Более общую формулировку Центральной предельной теоремы дал Линдеберг. Пусть X1, X2, , Xn – взаимно независимые случайные величины с функциями распределения F1(x), F2(x),…, Fn.(x). Пусть M(Xk)=Mk, , и дисперсии малы по сравнению с суммой (при любом e > 0 и всех достаточно больших N ). Тогда распределение нормированной суммы

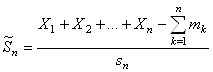стремится к стандартному нормальному распределению.

Пример 2. Вернемся к примеру 4 из $12 второй главы. Почему оценка на письменном тестировании по математике имеет нормальное распределение?

Оценка X складывается из N оценок X1, X2,…, Xn за каждую задачу. Случайная величина Xk имеет распределение в соответствии с трудностью К-ой задачи c конечными математическим ожиданием Mk и дисперсией . При больших N выполнены все условия теоремы Линдеберга (на практике N ³ 12 cчитается достаточно большим), и следовательно, оценку X можно считать нормально распределенной случайной величиной со средним значением и диcперсией . ¨

Следствием из Центральной предельной теоремы является

Теорема Муавра-Лапласа. Если проводится N независимых опытов, в каждом из которых событие А может произойти с вероятностью P и не произойти с вероятностью Q = 1 – P, то справедливо соотношение

Где Y – число наступлений события А в N опытах, Ф(X) – функция распределения стандартного нормального закона, a, b – действительные числа.

Доказательство. Пусть Xi – число наступлений события А в I-ом опыте, I = 1, 2,..., N,

Обозначим

Cогласно Замечанию 2 к Теореме 1 распределение случайной величины

При cтремится к стандартному нормальному распределению. Отсюда,

§

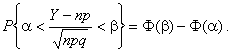Пример 3. Монету подбрасывают 200 раз. Какова вероятность, что число выпадений герба отличается от 100 не более чем на 5?

Применим теорему Муавра-Лапласа:

¨

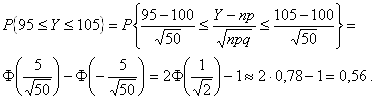< Предыдущая		Следующая >