13. Примеры непрерывных случайных величин
Пример 16. Равномерное распределение. Пусть на интервал (А, B) действительной прямой наугад бросают точку. Cлучайная величина Х – координата этой точки. Вероятность попадания точки на заданный интервал (Х1, X2) из (a, b) 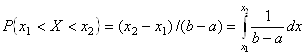 . Поэтому плотность распределения
. Поэтому плотность распределения
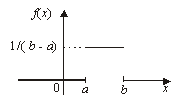
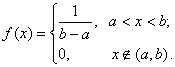
Такое распределение вероятностей называется Равномерным на интервале (a, b).
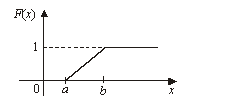 Функция распределения равномерного закона
Функция распределения равномерного закона 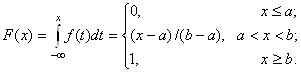
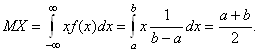
DX = M (X2) –(MX)2 = 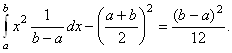
В примере 1 из пятого параграфа первой главы время прихода пассажира на платформу метрополитена имеет равномерное распределение в интервале (0, 4). ¨
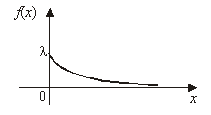 Пример 17. Показательное распределение. Cлучайная величина Х имеет Показательное распределение, если плотность распределения
Пример 17. Показательное распределение. Cлучайная величина Х имеет Показательное распределение, если плотность распределения
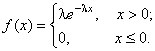
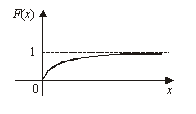
Функция распределения

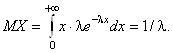
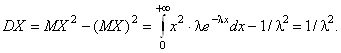
Показательное распределение часто имеют периоды ожидания или продолжительности “жизни” элементов (например, время до прихода автобуса или время “жизни” электрической лампочки). Показательное распределение обладает свойством отсутствия последействия: каков бы ни был настоящий “возраст” элемента, оставшееся время “жизни” не зависит от прошлого и имеет то же самое распределение, что и само время “жизни”. Отсутствие последействия присуще только показательному распределению. ¨
 Пример 18. Нормальное распределение. Непрерывное распределение с плотностью
Пример 18. Нормальное распределение. Непрерывное распределение с плотностью 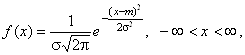 называется Нормальным распределением .
называется Нормальным распределением .
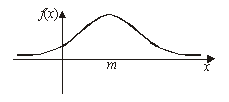
Графиком плотности является
Так называемая гауссова кривая.
Она симметрична относительно параметра M.
Параметр M также совпадает с математическим ожиданием нормально распределенной случайной величины, т. к. 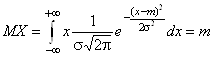 .
.
Cо вторым параметром s совпадает среднее квадратическое отклонение, поскольку 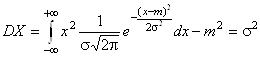 .
.
В силу симметричности плотности нормального распределения относительно математического ожидания любой центральный момент нечетного порядка равен нулю. следовательно, коэффициент асимметрии нормального распределения
АХ = ![]()
Для нормального распределения отношение ![]() . равно 3. Это отношение принимают за эталон для всех распределений и величину
. равно 3. Это отношение принимают за эталон для всех распределений и величину ![]() Называют Коэффициентом эксцесса. Коэффициент эксцесса характеризует островершинность распределения. Для нормального закона он равен нулю. Для более островершинных распределений коэффициент эксцесса положительный, для менее островершинных - отрицательный.
Называют Коэффициентом эксцесса. Коэффициент эксцесса характеризует островершинность распределения. Для нормального закона он равен нулю. Для более островершинных распределений коэффициент эксцесса положительный, для менее островершинных - отрицательный.
Нормальное распределение с параметрами M = 0 и s = 1 называется Стандартным нормальным распределением. Плотность стандартного нормального распределения
![]()
График плотности симметричен относительно нуля. ¨
| < Предыдущая | Следующая > |
|---|