05. Геометрические вероятности

Cогласно классическому определению, в опытах с конечным числом равновозможных исходов вероятность события А - это «доля» исходов, которые приводят к наступлению события А в общем количестве исходов. Определять вероятность как «долю» благоприятных исходов можно и в опытах с бесконечным числом исходов. Рассмотрим примеры подсчета так называемых «геометрических» вероятностей.

Пример 4. Поезда в метро отправляются со станции с интервалом в 4 минуты. Какова вероятность, что пассажир, пришедший на платформу, отправится с нее не позже, чем через 1,5 минуты?

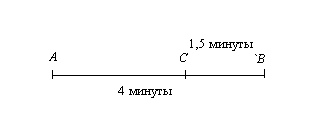подпись: Пространство элементарных исходов состоит из бесконечного множества точек отрезка [А, В] (см. рисунок), так как пассажир может появиться на платформе в любой момент между отправлениями поездов. Однако отправиться не позже, чем через полторы минуты, он сможет, если время его прихода попадет на отрезок [C, В]. Долей точек отрезка [C, В] в отрезке [А, В] можно считать отношение длин этих отрезков. Таким образом, искомая вероятность Р(А) = |В – C| / |B – А| = 1,5/4 = = 3/8.¨

подпись: Пример 5. Два человека независимо друг от друга решили отдохнуть в любую неделю февраля на одном и том же горнолыжном курорте. Какова вероятность, что они там встретятся?

Введем двумерную декартову систему координат XOY. Пусть пространство элементарных событий Ω={X,Y}, , где X – время (в сутках) приезда на курорт первого отдыхающего, а Y - второго.

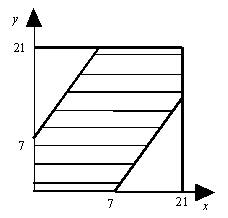
Графически пространству Ω соответствует квадрат со стороной, равной 21. Чтобы отдыхающие встретились, разность между Х и Y должна быть не более 7 суток, т. е. |X - Y| £ 7 или – 7 £ у – Х £ 7. Графически этому событию соответствует фигура, координаты точек которой удовлетворяют неравенству

X – 7 £ y £ X + 7. Искомая вероятность равна отношению площади заштрихованной фигуры к площади всего квадрата:

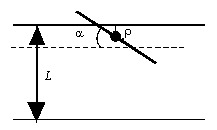подпись: Пример 6. Задача Бюффона. На плоскость, разлинованную линиями, параллельными оси ОХ и отстоящими друг от друга на расстояние L, наугад бросают иголку длины L (L < L). Какова вероятность того, что иголка пересечет одну из линий?

Будем считать иголку отрезком длины L. Пусть α - угол наклона этого отрезка к оси ОХ, ρ – расстояние от середины иглы до ближайшей линии, 0 £ α < π, 0 £ ρ £ L/2. Игла пересечет одну из линий тогда и только тогда, когда ρ £ L/2*(sin α).

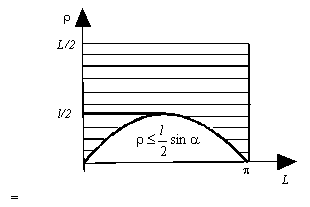подпись: Введем двумерную систему координат a0r. Пространство элементарных исходов представляет собой прямоугольник, cоставленный из точек {(a, r), 0 £ α < π, 0 £ ρ £ L/2}.

Благоприятные исходы – это множество точек этого прямоугольника, которые расположены не выше синусоиды. Доля таких точек в прямоугольнике может быть определена как отношение площади под синусоидой к площади прямоугольника. Следовательно,

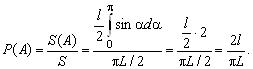< Предыдущая		Следующая >