§7. Ряды и интегралы Фурье. Тригонометрический ряд Фурье

Определение: Функция определённая на всей числовой прямой называется периодической, если .

Система функций: – такая система функций называется тригонометрической системой функций. Основной вопрос состоит в следующем: можно ли периодическую функцию с периодом 2π представить в виде линейной комбинации функций периодической системы? Далее будут установлены достаточные условия того, когда периодическая функция может быть представлена в указанном виде:

Равенство (1) называется разложением функции в тригонометрический ряд Фурье, коэффициенты и называются коэффициентами Фурье функции . Выведем формулы для и . Для этого будем считать, что задана на сегменте . Отметим свойство ортогональности тригонометрической системы функций: ; ;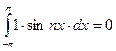

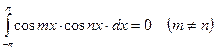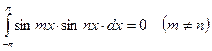; ; В пространстве функций, заданных на сегменте можно ввести скалярное произведение функций следующим образом: 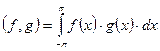; , – ограниченные. Таким образом интеграл по сегменту от произведения любых двух функций тригонометрической системы равен нулю. Будем предполагать, что для функции справедливо равенство (1)и что ряд Фурье (правая часть равенства (1)) можно почленно интегрировать. Проинтегрируем равенство (1) и соответственно получим:

Умножим равенство (1) на и получаем: . Аналогично получаем, что 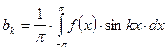. Окончательно получаем формулы для , и :

; ; .

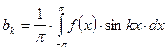Теорема: Если функция периодическая функция с периодом , то для любого числа Имеет место следующее равенство: 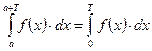, т. е. интеграл по любому сегменту длиной в период имеет одно и тоже значение.

Док-во: 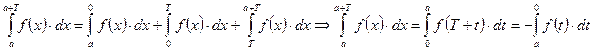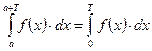, ч. т.д.

< Предыдущая		Следующая >