§7.2. Поточечная сходимость тригонометрического ряда Фурье
Определение: Функция ![]() называется кусочно-непрерывной на сегменте
называется кусочно-непрерывной на сегменте ![]() , если она непрерывна во всех точках сегмента
, если она непрерывна во всех точках сегмента ![]() за исключением, быть может, конечного числа точек в которых она имеет разрыв первого рода.
за исключением, быть может, конечного числа точек в которых она имеет разрыв первого рода.
Определение: Кусочно-непрерывная на сегменте ![]() функция называется кусочно-гладкой, если производная этой функции
функция называется кусочно-гладкой, если производная этой функции ![]() существует и непрерывна всюду на сегменте
существует и непрерывна всюду на сегменте ![]() за исключением, быть может, конечного числа точек, в которых существует правый и левый предел функции.
за исключением, быть может, конечного числа точек, в которых существует правый и левый предел функции.
Лемма 1: (Лемма об аппроксимации непрерывной на сегменте ![]() функции). Пусть функция
функции). Пусть функция ![]() непрерывна на сегменте
непрерывна на сегменте ![]() , тогда для любого
, тогда для любого ![]() существует непрерывная, кусочно-гладкая функция
существует непрерывная, кусочно-гладкая функция ![]() , такая, что для любого
, такая, что для любого ![]() из сегмента
из сегмента ![]() выполняется условие, что
выполняется условие, что ![]() , причём
, причём ![]() .
.
Лемма 2: Если функция ![]() – кусочно-непрерывна на сегменте
– кусочно-непрерывна на сегменте ![]() , то:
, то: 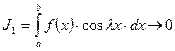 при
при ![]() ,
, 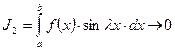 при
при ![]() .
.
Теорема: (О сходимости тригонометрического ряда Фурье в каждой точке). Пусть ![]() – кусочно-гладкая функция на сегменте
– кусочно-гладкая функция на сегменте ![]() . Тогда
. Тогда ![]() – сходится в точке
– сходится в точке ![]() и для его суммы
и для его суммы ![]() справедливо:
справедливо: ![]()
|
|
![]() Док-во: Продолжим периодически функцию
Док-во: Продолжим периодически функцию ![]() на всю числовую прямую с периодом
на всю числовую прямую с периодом ![]() и составим частичную сумму Фурье ряда:
и составим частичную сумму Фурье ряда: ![]() . Т. к.
. Т. к. 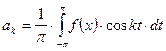 ;
; 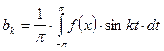 , то частичную сумму ряда можно переписать в следующей форме:
, то частичную сумму ряда можно переписать в следующей форме: 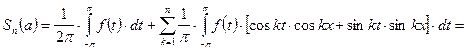
 (где
(где ![]() – ядро Дирихле порядка
– ядро Дирихле порядка ![]() (где
(где ![]() обозначает количество слагаемых, которые мы выбираем в исходной частичной сумме ряда Фурье))
обозначает количество слагаемых, которые мы выбираем в исходной частичной сумме ряда Фурье)) 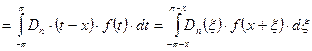 , где
, где ![]() , где
, где ![]() . Функции
. Функции ![]() и
и ![]() представляют собой периодические функции с периодом
представляют собой периодические функции с периодом ![]() .
. 
![]() . Далее рассмотрим:
. Далее рассмотрим:  .
.
Т. к. ![]() - чётная функция, то
- чётная функция, то  ; (умножим на
; (умножим на ![]()
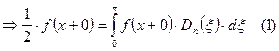
Рассмотрим частичную сумму: 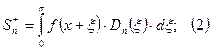 . Рассмотрим разность (2)-(1):
. Рассмотрим разность (2)-(1):  . Преобразуем ядро Дирихле
. Преобразуем ядро Дирихле ![]() :
: ![]() . Домножим на
. Домножим на ![]() и
и ![]() и получим:
и получим: ![]()
![]()
![]()
 .
.
Заметим, что выражение для ![]() не определено в точке
не определено в точке ![]() , но с другой стороны предел в данной точке равен:
, но с другой стороны предел в данной точке равен:  . Таким образом:
. Таким образом: 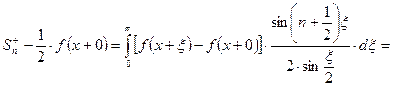
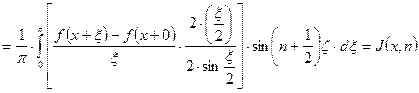 . По лемме 2
. По лемме 2 ![]() при
при ![]() , и аналогично:
, и аналогично: ![]() при
при ![]() , следовательно, складывая два последних результата, получаем:
, следовательно, складывая два последних результата, получаем: ![]() при
при ![]() , т. е.
, т. е. ![]() . Отметим, что если функция
. Отметим, что если функция ![]() непрерывна в точке
непрерывна в точке ![]() и односторонние пределы совпадают, значит
и односторонние пределы совпадают, значит ![]() , тем самым пункт (1) теоремы доказан.
, тем самым пункт (1) теоремы доказан.
2) Для значений в точках ![]() и
и ![]() запишем:
запишем: ![]()
![]()
![]()
![]() , тем самым пункт (2) теоремы доказан.
, тем самым пункт (2) теоремы доказан.
Комплексная форма ряда Фурье
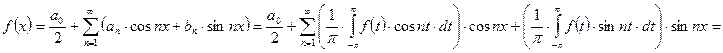
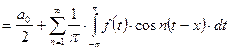 . Но
. Но 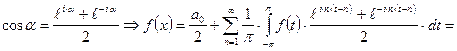

![]() . Итак
. Итак ![]() , где
, где 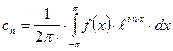 . Тем самым мы получили разложение функции
. Тем самым мы получили разложение функции ![]() по системе функций
по системе функций ![]() . Указанная система функций является ортогональной на сегменте
. Указанная система функций является ортогональной на сегменте ![]() , то есть
, то есть  .
.
| < Предыдущая | Следующая > |
|---|