§4.3. Несобственные интегралы второго рода
Пусть функция ![]() определена на полусегменте
определена на полусегменте ![]() будем считать, что функция
будем считать, что функция ![]() является не ограниченной на этом полусегменте. При этом на сегменте
является не ограниченной на этом полусегменте. При этом на сегменте ![]() функция является ограниченной (при этом
функция является ограниченной (при этом ![]() ). Точку А назовем особой точкой функции
). Точку А назовем особой точкой функции ![]() и рассмотрим интеграл:
и рассмотрим интеграл: 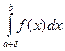 .
.
Понятно, что значение данного интеграла будет зависеть от ![]() И рассмотрим предел при
И рассмотрим предел при ![]() значения этого интеграла.
значения этого интеграла.
В независимости от этого указанный предел будем называть несобственным интегралом II рода на полусегменте ![]() .
.
Если указанный предел существует, то говорят, что несобственный интеграл сходится.
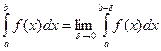
Если особая точка c является внутренней точкой промежутка разбиения, то есть ![]()
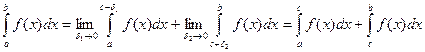 .
.
Пример 1:
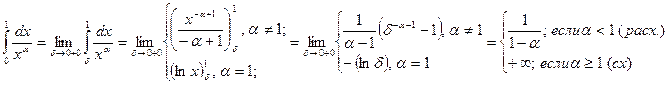
Теорема (Критерий Коши): Для того чтобы несобственный интеграл 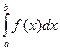 сходился на
сходился на ![]() необходимо и достаточно, чтобы
необходимо и достаточно, чтобы ![]() такое
такое ![]() , что
, что ![]()
Выполнялось условие: 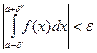 .
.
Справедливость этого утверждения вытекает из того, что сходимость несобственного интеграла означает существование предела ![]()
Признак сравнения: Если функции ![]() и
и ![]() удовлетворяют условию
удовлетворяют условию ![]() при
при ![]() И существуют интегралы
И существуют интегралы
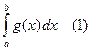
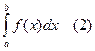
То из сходимости (1) следует сходимость (2), а из расходимости (2) следует соответственно расходимость (1).
Следствие: Если![]() ,
, ![]() при
при ![]() И
И ![]() , то интегралы
, то интегралы
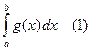
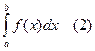
Сходятся и расходятся одновременно.
Пример 2:
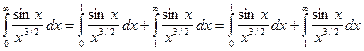 – сходится.
– сходится.
Главное значение несобственного интеграла
Пример:
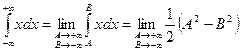
Полученный предел очевидно не существует. Пусть![]() , тогда указанный интеграл:
, тогда указанный интеграл:
![]()
Пусть ![]() определена на
определена на ![]() И пусть функция
И пусть функция ![]() интегрируема на любом сегменте.
интегрируема на любом сегменте.
Определение: Если существует предел ![]() , то он называется главным значением несобственного интеграла
, то он называется главным значением несобственного интеграла ![]() в смысле Коши и обозначается следующим образом:
в смысле Коши и обозначается следующим образом:
![]() (V.P. = Vabeur principal).
(V.P. = Vabeur principal).
В этом случае говорят, что функция ![]() интегрируема на прямой
интегрируема на прямой ![]() . Очевидно, что если несобственный интеграл
. Очевидно, что если несобственный интеграл ![]() сходится, то его значение совпадает с его собственным значением. Но может так быть, что несобственный интеграл расходится, но при этом имеет конечное главное значение.
сходится, то его значение совпадает с его собственным значением. Но может так быть, что несобственный интеграл расходится, но при этом имеет конечное главное значение.
Рассмотрим несобственный интеграл второго рода 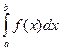 , где C – внутренняя особая точка интервала
, где C – внутренняя особая точка интервала ![]() .
.
Определение: Если существует предел «конструкции» следующего вида: 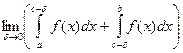 ,
,
То он называется главным значением несобственного интеграла второго рода 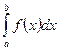 И обозначается V.P.
И обозначается V.P. 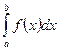 .
.
Отметим, что исходный несобственный интеграл может быть расходящимся, то есть может не существовать предел 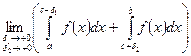 .
.
Пример:
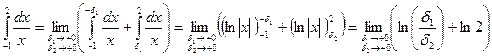 не существует.
не существует.
Вычислим интеграл в смысле главного значения:
V.P. 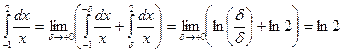 .
.
| < Предыдущая | Следующая > |
|---|