§1.6. Формула Стокса

Определение: Пусть – регулярное множество и пусть заданы функции . Будем рассматривать векторное поле . Будем называть ротором вектор-функции:

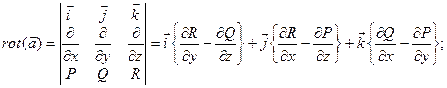
Теорема (Стокса) Пусть Ф – полная, ограниченная, кусочно-гладкая, ориентированная поверхность, причем указана ориентация , – край поверхности Ф, состоит из конечного числа замкнутых кусочно-гладких кривых и на задано положительное направление обхода. Пусть - некоторая окрестность поверхности Ф, в ней заданы гладкие функции . Тогда справедлива следующая формула:

< Предыдущая		Следующая >