§1.5. Формула Остроградского-Гаусса

Определение: Будем говорим, что Ф – замкнутая поверхность, если Ф – полная ограниченная поверхность без границ.

Определение: Дивергенцией векторного поля называется скаляр, который в декартовых координатах имеет вид:

Теорема (Остроградского-Гаусса): Пусть – регулярное, замкнутое, ограниченное, кубируемое множество. Пусть граница этого множества состоит из конечного числа замкнутых, кусочно-гладких ориентированных поверхностей; и будем считать, что на границе выбрана единичная нормаль , внешняя по отношению к области D.

Если все три этих условия выполнены, то справедливо следующее равенство:

Док-во: Докажем теорему для случая, когда D – простая область. Нам надо доказать только одно равенство, так как другие доказываются аналогично.

D – Z-трапециевидная область

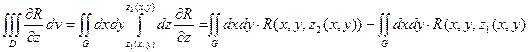– по формуле Ньютона-Лейбница.

То есть для z – трапецеидальной области формула (2) справедлива. Докажем теперь формулу для простой области D. Разобьем область D на сумму конечного числа z-трапецеидальных областей:

, ч. т.д.

< Предыдущая		Следующая >