§5. Криволинейные интегралы. Криволинейные интегралы первого рода
Рассмотрим плоскость XOY и кривую L на ней:
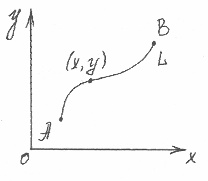

Опр.: Кривая L называется простой незамкнутой кривой, если различным значениям параметра T соответствуют различные точки кривой L.
Опр.: Кривая L называется простой замкнутой кривой, если точки ![]() .
.
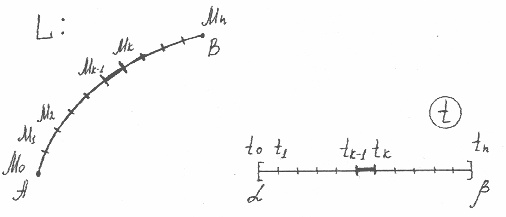
Опр.: Кривая L Называется спрямляемой, если существует предел длин ломаных, вписанных в данную кривую при ![]() , где
, где ![]() – длина наибольшего звена ломаной.
– длина наибольшего звена ломаной.
Пусть функция F(X, Y) Задана на кривой L, т. е. F(X, Y) Задана во всех точках плоскости, принадлежащих данной кривой.
Рассмотрим разбиение сегмента ![]() на N Элементарных сегментов.
на N Элементарных сегментов.
Указанное разбиение влечет соответствующее разбиение кривой L На элементарные дуги
![]() .
.
Составим интегральную сумму:
![]() ,
,
Где ![]()
Пусть ![]()
Опр.: Число I называется пределом интегральной суммы при ![]() , если
, если ![]() такое, что для любого разбиения, удовлетворяющего условию
такое, что для любого разбиения, удовлетворяющего условию ![]() , выполняется
, выполняется
![]()
Для любого выбора точек Nk на сегменте разбиения.
Если I существует, то он называется криволинейным интегралом первого рода и обозначается
![]() Или
Или ![]() .
.
Замечание. Значение криволинейного интеграла I рода не зависит от «направления разбиения»: нумерация точек разбиения может идти как от A к B, так и наоборот.
Поэтому ![]() .
.
| < Предыдущая | Следующая > |
|---|