§3. Определенный интеграл. Понятие определенного интеграла
Рассмотрим функцию ![]() , определенную на сегменте
, определенную на сегменте ![]() .
.
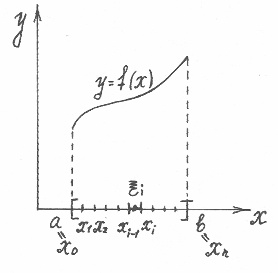
Рассмотрим разбиение ![]() на n элементарных сегментов. Таким образом получается n сегментов вида
на n элементарных сегментов. Таким образом получается n сегментов вида ![]() , где
, где
![]() .
.
Разбиение будем обозначать: ![]() -разбиение сегмента
-разбиение сегмента ![]() ,
,
![]() -длина элементарного сегмента разбиения.
-длина элементарного сегмента разбиения.
![]() .
.
Составим интегральную сумму.
Опр. Интегральная сумма-это сумма вида
![]() ,
,
![]() -некоторая точка, принадлежащая
-некоторая точка, принадлежащая ![]() .
.
Интегральная сумма ![]() зависит от данного разбиения сегмента
зависит от данного разбиения сегмента ![]() и выбора точек
и выбора точек ![]() на каждом отдельном элементарном сегменте разбиения.
на каждом отдельном элементарном сегменте разбиения.
Опр. Если все элементарные сегменты разбиения являются равными, то такое разбиение называется равномерным.
![]() - длина максимального элементарного отрезка в конкретном разбиении.
- длина максимального элементарного отрезка в конкретном разбиении.
Опр. Пределом интегральных сумм при ![]() , называется число
, называется число ![]() , такое, что если
, такое, что если ![]() , то
, то
![]()
Для любого выбора точек ![]() на каждом элементарном сегменте данного разбиения.
на каждом элементарном сегменте данного разбиения.
![]()
Опр. Функция ![]() , заданная на сегменте, называется Интегрируемой на данном сегменте (по Риману), если для какого-либо разбиения данного сегмента существует предел предел интегральных сумм. Предел интегральных сумм называется определенным интегралом.
, заданная на сегменте, называется Интегрируемой на данном сегменте (по Риману), если для какого-либо разбиения данного сегмента существует предел предел интегральных сумм. Предел интегральных сумм называется определенным интегралом.
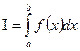
| < Предыдущая | Следующая > |
|---|