§2.8. Методы исследования условного экстремума

I. Метод исключения части переменных

Пример:

Исследуем на экстремум (1)

(2)

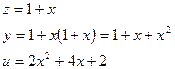
Таким образом задача (1, 2) на условный экстремум сведена к задаче на безусловный локальный экстремум.

Замечание:

По существу условие связи (2) задают неявных функций.

II. Метод Лагранжа.

Теорема

1) Пусть функция (1) дифференцируема в некоторой точке и имеет в этой точке условный экстремум при выполнении условий связи (2).

2) Будем считать, что система (2) удовлетворяет всем требованиям теоремы о существовании неявных функций.

Тогда в указанной точке для частичных производных функции Лагранжа

(функция Лагранжа) (3)

Выполняются условия, что

,

Где -некоторые коэффициенты.

.

В тех точках, в которых выполняются условия связи (2), функция Лагранжа

.

Задачи исследования функции на условный экстремум для функции m переменных сводится к задаче на исследование на безусловный экстремум функции Лагранжа, зависящей от m+k переменных.

Пример:

Исследовать на условный экстремум методом Лагранжа

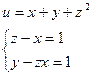
Функция Лагранжа

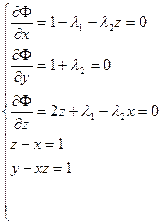, решение: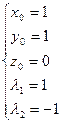

Для выяснения характера экстремума необходимо исследовать второй дифференциал функции Лагранжа, как это делалось для обычной функции.

 

< Предыдущая		Следующая >