§3.10. Теорема о замене переменных
J – Некоторый промежуток;
J Î C(J);
A¹B;
[a, b] Í J;
A¹B;
Y Î С1([A,B]);
Y(A)=a;
Y(B)=b;
Y(t) Î J При t Î [A,B].
Тогда 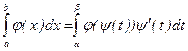
Док-во:
Т. к. J Î C(J);
J Î C1([A,B])
Þ {J(Y(t))Y′(t)} Í C([A,B]).
В силу теоремы о $ первообразной непрерывной функции $ F – первообразная J На J.
Тогда F(Y(t)) – первообразная функции J(Y(t))Y′(t) на J.
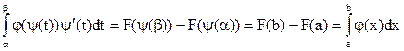
ч .т. д.
В этой теореме реально используется:
· J Î С([a, b])
· {J(Y(t))Y′(t)} Í C1([A,B]).
· J имеет первообразную на J
· Y дифференцируема на [A,B]
| < Предыдущая | Следующая > |
|---|