§2.6. Функциональные матрицы

Опр. Функциональной для системы (1) называется матрица:

Функциональная матрица имеет размерность m*n.

Теорема 2

1) Пусть функции (1) дифференцируемы в некоторой окрестности точки , а их частные производные Непрерывны в точке.

2) Пусть минор r-го порядка в точке Не равен 0.

3) Все миноры r+1-го порядка равны 0 в окрестности wM0.

Тогда функции (1) являются зависимыми, причем r функций из указанного минора r-го порядка выражаются через остальные функции.

Доказательство провести самостоятельно.

Пример:

Исследуем вопрос о зависимости функций :

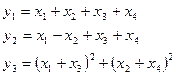
Составим функциональную матрицу

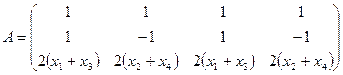
Воспользуемся теоремой 2. Минор второго порядка

Любой минор третьего порядка равен 0, т. к. будет содержать два одинаковых столбца. Следовательно,. Третью функцию можно выразить через первые две:

.

< Предыдущая		Следующая >