§2.2. Теорема о существовании и дифференцируемости неявной функции и некоторые ее применения
Теорема 1.
Пусть:
1) Функция ![]() непрерывная в прямоугольнике
непрерывная в прямоугольнике ![]()
2) Для ![]() выполнено условие
выполнено условие ![]() (т. е. на верхней и нижней стороне прямоугольника функция
(т. е. на верхней и нижней стороне прямоугольника функция ![]() принимает значения различных знаков).
принимает значения различных знаков). 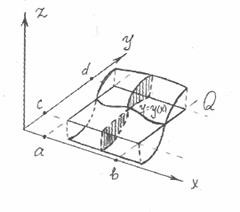
3) Для ![]() - является строго монотонной по переменной
- является строго монотонной по переменной ![]() на всем отрезке
на всем отрезке ![]()
Тогда существует единственная функция неявная функция ![]() , определяемая условием (1) (
, определяемая условием (1) (![]() ) , непрерывная на интервале
) , непрерывная на интервале![]() .
.
Неявная функция наглядно показывается пересечением поверхности ![]() и плоскости
и плоскости ![]()
Теорема 2.
Пусть:
1) функция ![]() дифференцируема в некоторой окрестности
дифференцируема в некоторой окрестности ![]() точки
точки ![]()
![]() .
.
2) Пусть частная производная ![]() - непрерывная в точке
- непрерывная в точке ![]() .
.
3) Пусть![]() ,
, ![]() .
.
(угадали “одну точку из решения”).
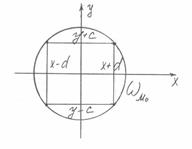
Тогда существует прямоугольник: ![]() целиком лежащей в окрестности
целиком лежащей в окрестности ![]() В котором существует единственная неявная функция
В котором существует единственная неявная функция ![]() , удовлетворяющая условию (1) и дифференцируемая на интервале (x – d, x +d).
, удовлетворяющая условию (1) и дифференцируемая на интервале (x – d, x +d).
При этом производная неявной функции вычисляется по следующей формуле:
![]() (3)
(3)
Точка ![]() принадлежит графику функции и производная не равна нулю.
принадлежит графику функции и производная не равна нулю.
Замечание (о порядке вычисления производной):
В формуле (3) сначала формально вычисляются производные ![]() ,
, ![]() и лишь затем подставляется
и лишь затем подставляется ![]() .
.
Пример 1
![]()
![]() (1)
(1)
Доказать, что![]() и найти
и найти ![]() ,
, ![]()
![]()
Докажем, что ![]() существует (предполагаем, что
существует (предполагаем, что ![]() ).
).
Если при фиксированном ![]() При достаточно больших значениях
При достаточно больших значениях ![]() , очевидно выполняются неравенства
, очевидно выполняются неравенства ![]() < 0 при
< 0 при ![]() при
при ![]() .
.
Отсюда следует, что по теореме 1 существует единственная неявная функция.
В контексте теоремы 1 прямоугольник превращается в бесконечную плоскость.
Очевидно, что ![]() является дифференцируемой на всей области определения.
является дифференцируемой на всей области определения.
Так как ![]() - непрерывная функция и если
- непрерывная функция и если ![]() , то
, то ![]()
![]()
![]() , т. е. выполнены условия теоремы 2.
, т. е. выполнены условия теоремы 2.
 из этого следует
из этого следует
![]()
Полученное соотношение позволяет вычислять значение производной в данной точке по уже известному значению самой функции в данной точке.
Формулы для вычисления производной в данной точке позволяют только (но и это не мало) по указанному значению функции в данной точке посчитать значения производных разных порядков в данной точке.
![]()
![]()
Руководство:
Вторая производная от неявной функции вычисляется как производная от первой производной.
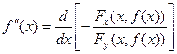
При условии, что ![]() вычисляется на неявной функции.
вычисляется на неявной функции.
![]()
В результате производная любого порядка должна зависеть только от значения ![]() в точке.
в точке.
Пример 2
![]() Найти
Найти ![]()
![]() (1)
(1)
Два способа :
1 – стандартный способ (смотри предыдущий пример)
2 – существует неявная функция в выражении (1); тогда (1) превращается в тождество и его можно дифференцировать по X:
![]() (2)
(2)
Если ![]() то
то ![]()
![]()
![]()
Для нахождения второй производной, еще раз продифференцируем соотношение (2):
![]() учитывая, что
учитывая, что ![]() получим
получим
![]() .
.
Можно восстановить функцию по формуле Тейлора, зная ![]()
| < Предыдущая | Следующая > |
|---|