§1.27. Отступление. Понятие квадратичной формы

Опр. Квадратичной формой называется функция нескольких переменных следующего вида:

Опр. Квадратичная форма называется положительно определенной, если >0 при всех значениях , кроме

Любая квадратичная форма в нуле всегда равна нулю.

Опр. Квадратичная форма называется отрицательно определенной, если <0 при всех значениях , кроме

Если квадратичная форма является либо положительно определенной, либо отрицательно определенной, то она называется знакоопределенной.

Исследование квадратичной формы на знакооопределенность. Критерий Сильвестра

Матрице квадратичной формы:

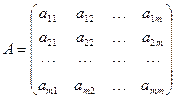
Угловыми минорами называются определители вида: (см. рисунок).

Для того чтобы квадратичная форма Q Была положительно определенной необходимо и достаточно, чтобы все (Q>0).

Для того чтобы квадратичная форма Q Была отрицательно определенной необходимо и достаточно, чтобы знаки угловых миноров чередовались (Q<0).

Достаточное условие локального экстремума

Пусть функция U=F(M) дифференцируема в окрестности точки М0 и дважды дифференцируема в самой точке М0. Пусть

Тогда, если второй дифференциал функции U В точке М0, представляет собой в данной точке положительно определенную квадратичную форму по переменным , то М0 – точка локального минимума.

Если второй дифференциал является отрицательно определенным в точке М0, тогда М0 – точка локального максимума.

Если второй дифференциал представляет собой знакопеременную квадратичную форму в точке М0, тогда М0 – не является точкой локального максимума или минимума.

Пример:

Исследовать на локальный экстремум

I Необходимое условие:

Решая систему, находим

II Достаточное условие

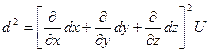
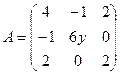
Для точки М1:

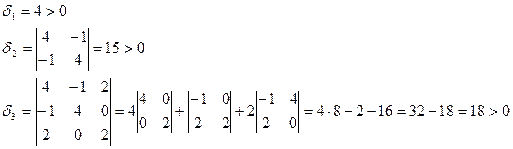
Следовательно второй дифференциал представляет собой положительно определенную квадратичную форму, значит М1 – точка локального минимума.

< Предыдущая		Следующая >