§1.26. Необходимое условие локального экстремума

Пусть функция F(M) дифференцируема в точке М0 и в точке существует первая производная этой функции. Пусть точке М0 является точкой локального экстремума, тогда

Необходимым условием локального экстремума является равенство нулю всех первых производных (или равенство нулю первого дифференциала).

Док-во:

Докажем, что .

Фиксируем значение всех координат и проследим характер изменения функции по переменной .

Тогда поскольку F(M) Удовлетворяет условию локального экстремума, то она должна удовлетворять условию локального экстремума по , т. е.

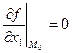
Аналогично доказывается, что все остальные частные производные равны нулю.

ч. т. д.

< Предыдущая		Следующая >