24. Линейная регрессия
Линейная регрессия является простейшим видом регрессии. Классическим алгоритмом линейной регрессии является метод наименьших квадратов. В котором критерием является минимизация суммы квадратов отклонений аппроксимирующей функции от заданных точек:
![]() .
.
Существуют и другие алгоритмы определения коэффициентов линейной регрессии – метод медиан.
В общем виде аппроксимирующею функцию можно представить как ![]() . Задачей линейной регрессии является вычисление параметров a и b. Для этого в MathCad существует ряд встроенных функций (где VX, VY – вектора узловых точек):
. Задачей линейной регрессии является вычисление параметров a и b. Для этого в MathCad существует ряд встроенных функций (где VX, VY – вектора узловых точек):
1. corr(VX, VY) – возврящает скаляр – коэффициент корреляции Пирсона. Чем ближе коэффициент к 1 тем точнее исходная зависимость приближается к линейной;
2. intercept(VX, VY) – возвращает значение параметра а (свободный член) рассчитанного методом наименьших квадратов;
3. slope(VX, VY) – определяет значение параметра b (угловой коэффициент) рассчитанного методом наименьших квадратов;
4. line(VX, VY) – [MathCAD 2000] возвращает вектор первый элемент которого параметр а, второй b рассчитанные по методу наименьших квадратов;
5. medfit(VX, VY) – [MathCAD 2000] возвращает вектор первый элемент которого параметр а, второй b рассчитанные по методу медиан.
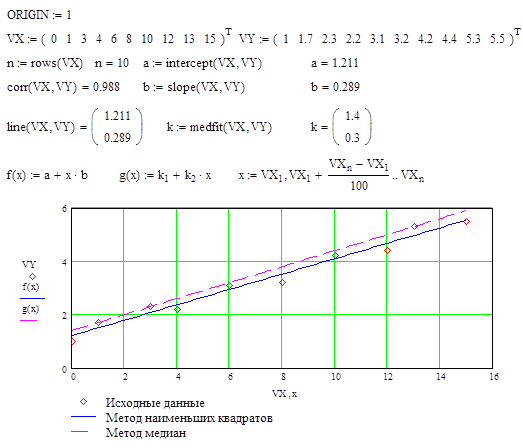
Как видно из примера при аппроксимации линейной регрессией прямая проходит через "облако" точек.
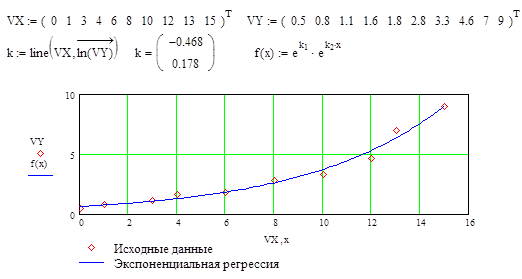
Используя встроенные функции можно рассчитывать регрессию не только для линейных, но и для экспоненциальных функций ![]() . Для этого f(x) с помощью логарифмирования по натуральному основанию приводится к линейной. Рассчитанный коэффициент а, полученный в логарифмической форме, затем пересчитывается.
. Для этого f(x) с помощью логарифмирования по натуральному основанию приводится к линейной. Рассчитанный коэффициент а, полученный в логарифмической форме, затем пересчитывается.
| < Предыдущая | Следующая > |
|---|