3.10.1. Сети. Основные понятия

Сетью (в самом общем смысле) называется всякий граф, в котором специально выделены некоторые вершины, называемые полюсами. Например, корневое дерево можно рассматривать как однополюсную сеть (полюс – корень).

В данном параграфе под сетью мы будем понимать взвешенный ориентированный граф.

Примерами таких сетей являются схемы улиц, нефте-, газо - и трубопроводов, линий электропередач (в качестве веса может выступать пропускная способность); схемы выполнения комплекса работ при подготовке какого-либо мероприятия, проекта, строительства дома, завода и т. д. (вес -- время выполнения работ или их стоимость, в зависимости от решаемой задачи).

Для сетей полустепень исхода V Вершины V определяется как сумма весов всех дуг, для которых V Является началом, а полустепень захода V -- сумма весов всех дуг, для которых V Является концом.

Как и для обычных орграфов, для сетей справедлива

Лемма (о "рукопожатиях"). Сумма полустепеней исхода всех вершин сети равна сумме полустепеней захода.

В сети вершины, которые являются только началом дуг, называются Источниками, а вершины, которые являются только концами дуг – Стоками (это полюса сети).

Обычно рассматриваются сети без ориентированных циклов. В этом случае они представляют собой совокупность путей, ведущих от источников к стокам. Кроме того, можно считать, что в сети существует один источник и один сток. В противном случае, если сеть имеет несколько источников и несколько стоков , то сеть можно преобразовать, объединив все источники и объединив все стоки, или ввести

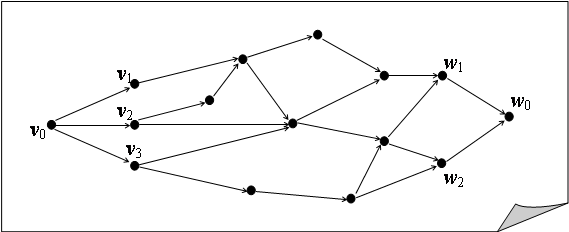фиктивный (общий) источник и сток , как на рисунке:

Сеть с одним источником и одним стоком называют (,)-сетью.

< Предыдущая		Следующая >